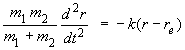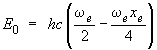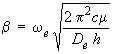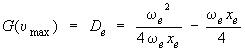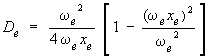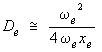|
|
|
|
MODULE 2 Vibration
des molécules diatomiques Préambule La molécule diatomique, la plus simple, peut effectuer plusieurs types de mouvements, dont la rotation et la vibration. Le mouvement de rotation fait l'objet du module 1. Le présent module concerne exclusivement le mouvement de vibration, dans lequel les atomes oscillent le long de la liaison interatomique. Comment peut-on observer ce mouvement moléculaire? Est-ce que l'application de la mécanique classique renseigne sur les lois qui gouvernent ce mouvement? L'introduction de la mécanique quantique est-elle nécessaire? Si oui, quelles en sont les conséquences sur l'interprétation des observations?
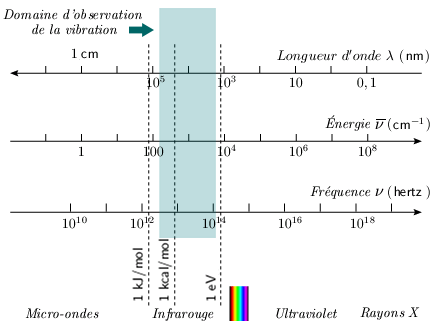
Faits expérimentaux On observe que les molécules diatomiques absorbent les radiations électromagnétiques dans l'infrarouge, soit dans le domaine de longueurs d'ondes comprises entre 1 et 100 μm (figure 2.1), donc dans les régions du proche infrarouge (1 à 5 μm), de l'infrarouge moyen (5 à 20 μm) et de l'infrarouge lointain. Cette absorption est reliée à la vibration des molécules.
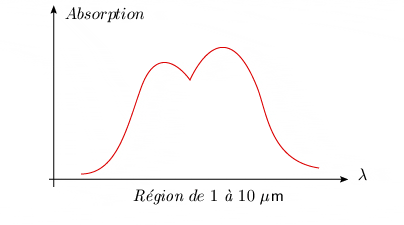
Si l'appareillage utilisé pour la spectroscopie possède une faible dispersion, comme celui que l'on emploie en analyse instrumentale, et si la couche de molécules est mince, le spectre d'absorption de vibration prend la forme d'une large bande appelée bande fondamentale.
Le tableau 2.1 présente la position de la bande fondamentale pour quelques molécules diatomiques courantes.
Tableau 2.1. Bandes
fondamentales de quelques
On observe d'autres bandes plus faibles, appelées harmoniques, à des fréquences doubles, triples, etc., quand on effectue des observations avec des couches plus épaisses. Ces observations exigent des épaisseurs de plusieurs mètres à pression atmosphérique, ou encore des cellules à miroirs parallèles qui augmentent la longueur du trajet optique. En première approximation, on peut représenter les fréquences caractéristiques de ces bandes d'absorption par une formule du type :
En réalité les intervalles entre les bandes successives ne sont pas égaux mais décroissent lentement, de sorte que la formule expérimentale correcte est :
Pour HCl par exemple on mesure : b = 2 937,30 cm–1 et c = 51,60 cm–1. Le tableau 2.2 présente les fréquences caractéristiques des bandes observées pour HCl, avec les différences de premier et de second ordre et les valeurs calculées à l'aide de l'équation 2.2. Tableau 2.2. Énergie des bandes d'absorption de HCl.
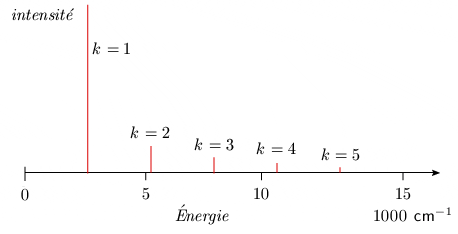
Par ailleurs, l'intensité de l'absorption des bandes diminue avec la fréquence, comme le montre la figure 2.3.
Modèle mécanique de l'oscillateur harmonique Le modèle le plus simple pouvant représenter la vibration d'une molécule est l'oscillateur harmonique. Un tel oscillateur est défini comme un point de masse m rappelé vers une position d'équilibre par une force, appelée force de rappel, proportionnelle à la distance du point à sa position d'équilibre (loi de Hooke). Plus précisément, si F est la force et k la constante de proportionnalité, appelée constante de rappel, la loi fondamentale de la mécanique (deuxième loi de Newton) permet d'écrire :
La solution de l'équation différentielle du mouvement est bien connue : x = x0 sin (2πvt + φ) v est la fréquence d'oscillation donnée par :
Un système moléculaire diatomique peut se ramener à ce schéma mécanique. Nous supposons que les deux atomes ne sont plus liés de façon rigide, mais peuvent osciller autour de leur position d'équilibre le long de l'axe internucléaire. Nous supposons également que la force de rappel est proportionnelle à l'élongation ce qui n'est, nous le verrons par la suite, qu'une première approximation. Si re est la distance internucléaire à l'équilibre (de vibration) et r la distance réelle des deux atomes au temps t on a, en appliquant la loi fondamentale de la mécanique à chacun des atomes :
r1 et r2 étant les positions, au même temps t, des atomes 1 et 2 par rapport au centre de masse de la molécule. Or, d'après la définition du centre de masse (voir module 1, équation 1.1b), on peut écrire :
Les équations 2.5a et 2.5b peuvent être combinées pour former une seule équation :
Cette équation peut également s'écrire :
équation de forme analogue à la relation 2.3. On peut donc considérer la molécule comme un oscillateur harmonique (c'est-à-dire un point matériel oscillant avec une force de rappel proportionnelle à l'élongation) dont la masse est la masse réduite de la molécule. Si l'on compare les équations 2.3 et 2.6, on voit que la fréquence angulaire d'oscillation ω (en rad/s ou s–1) et la fréquence v (en Hz ou s–1) sont données ici par :
Les constantes de force sont très variables d'une molécule à l'autre, comme le montre le tableau 2.3 qui donne les valeurs (en N/m) de cette constante pour quelques molécules diatomiques. Tableau 2.3. Vibration moléculaire et constante de force.
Lors de l'oscillation de la molécule, il y a continuellement transformation de l'énergie potentielle en énergie cinétique. On peut donc caractériser l'énergie du système par son énergie potentielle V. Celle-ci est liée à la force F par la relation :
L'expression de l'énergie potentielle est obtenue par l'intégration de cette relation, ce qui donne, si l'on suppose que V = 0 quand r = re :
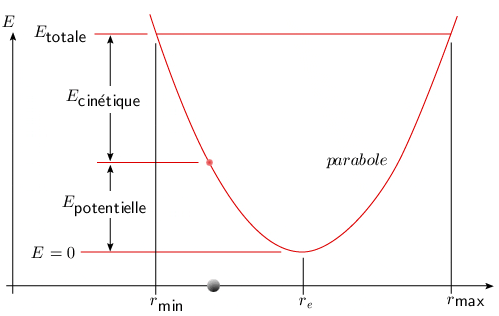
C'est l'équation d'une parabole avec un minimum nul pour r = re. L'énergie totale est égale à l'énergie potentielle pour une vitesse nulle, c'est-à-dire lorsque la masse atteint les positions d'élongation minimum ou maximum (figure 2.4).
En théorie classique, toutes les élongations sont possibles ainsi que toutes les valeurs de l'énergie. L'absorption ou l'émission de l'énergie par une molécule en vibration devrait être un phénomène continu. Voyons maintenant comment la mécanique quantique a permis de modifier cette conception.
Traitement quantique du modèle mécanique Selon la mécanique quantique, le mouvement de la molécule est décrit par l'équation de Schrödinger qui, dans ce cas, s'écrit :
E est l'énergie totale de la molécule et ψ (r) est la fonction d'onde, dont le carré du module donne la distribution de probabilité de la distance internucléaire r. La solution de cette équation fournit les valeurs possibles de l'énergie totale :
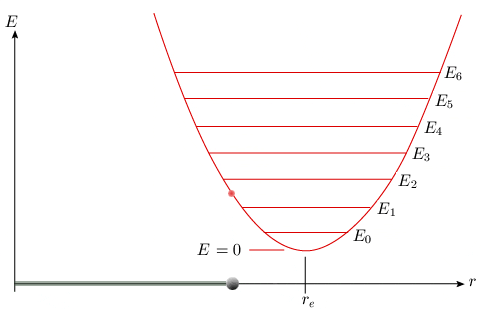
v est la fréquence de vibration et υ est un nombre quantique de vibration pouvant prendre les valeurs : υ = 0, 1, 2 . . . L'énergie de la molécule ne peut posséder que certaines valeurs bien définies; on parle alors de valeurs discrètes. Sur le diagramme représentant l'énergie potentielle (figure 2.5), les niveaux d'énergie totale possibles sont représentés par des lignes horizontales équidistantes. L'intersection de ces lignes horizontales avec la parabole représente les élongations minimale et maximale de la liaison, où l'énergie potentielle est égale à l'énergie totale.
Relation entre les fréquences de vibration et d'absorption La question que l'on peut se poser est la suivante : existe-t-il une relation entre la fréquence de la vibration de la molécule et la fréquence de la transition observée dans le spectre d'absorption? D'une part, rappelons que la fréquence de la vibration de la molécule, notée v dans les équations précédentes, est la même quel que soit le nombre quantique υ. Elle est donnée par la relation 2.7. D'autre part, la bande fondamentale en absorption est associée à la transition entre les niveaux υ = 0 et υ = 1; sa fréquence, (notée pour l'instant vbf) est reliée à la différence d'énergie entre ces deux niveaux par la relation de Planck-Einstein : Etransition = hvbf où h est la constante de Planck. D'après la relation 2.8, cette différence d'énergie est donnée par : Etransition = Eυ = 1 – Eυ = 0 = hv (3/2) – hv (1/2) = hv En comparant ces deux relations, on conclut que la fréquence de la bande fondamentale d'absorption vbf (en fait, de toute transition où le nombre quantique de vibration change d'une unité) est égale, selon un modèle classique, à la fréquence de vibration v de la molécule.
Spectre d'absorption de l'oscillateur harmonique Les variations d'énergie de la molécule peuvent seulement se produire entre les niveaux d'énergie totale possibles. La nécessité de variation du moment dipolaire pour qu'il y ait absorption ou émission de radiation impose des contraintes sur les transitions permises. Ces contraintes sont appelées règles de sélection. Ainsi, on peut montrer théoriquement que les seules transitions permises pour l'oscillateur harmonique doivent satisfaire la relation suivante : Δυ = ±1 Le signe ± indique que si la molécule peut absorber de la lumière, le chemin inverse est aussi possible : on observe alors le phénomène de l'émission et la règle de sélection devient Δυ = –1. L'énergie
où c est la vitesse de la lumière. Nous n'envisageons pas les transitions qui ne partent pas du niveau υ = 0 car à la température ordinaire (à laquelle ont lieu en général les expériences d'absorption) pratiquement toutes les molécules sont dans l'état υ = 0 . On représente le plus souvent la quantité v/c par ωe. Cette quantité, appelée constante d'harmonicité, représente en fait la fréquence de vibration propre de la molécule exprimée en nombre d'ondes, dont les unités sont des cm–1. Ce résultat théorique explique l'existence de la bande fondamentale caractéristique de chaque molécule, mais pas la présence des autres bandes que nous avons appelées harmoniques.
Perfectionnement du modèle quantique de l'oscillateur anharmonique Il est immédiatement évident que l'oscillateur harmonique est un modèle trop simple. Tout d'abord, toutes les fréquences expérimentales ne sont pas représentées. Ensuite, ce qui est plus grave, la fonction potentielle est certainement fausse. En effet, selon cette fonction, l'énergie potentielle croît indéfiniment à mesure que la distance internucléaire augmente. Si l'énergie potentielle était infinie pour des atomes très éloignés les uns des autres, on devrait pouvoir récupérer une énergie infinie lorsqu'on les rapproche jusqu'à la distance internucléaire. Inversement, il faudrait fournir une énergie infinie pour séparer les deux atomes. Or, on sait que cette dernière énergie est finie. C'est l'énergie de dissociation de la molécule. L'énergie potentielle réelle est donc représentée par une courbe qui n'est pas une parabole. La branche droite doit tendre asymptotiquement vers une valeur finie. Un pas dans cette direction peut être accompli en ajoutant une correction d'ordre cubique à la courbe de potentiel. Celle-ci est alors représentée par la formule suivante :
g étant un coefficient beaucoup plus petit que f. Au voisinage du minimum, cette nouvelle courbe se superpose avec la parabole précédente (voir animation de la figure 2.6), ce qui explique le succès partiel du premier modèle. Elle prévoit une valeur d'énergie plus grande que celui-ci à gauche du minimum, et plus petite à droite.
Cette courbe de potentiel est caractéristique d'un oscillateur anharmonique. Dans un tel oscillateur, la force de rappel n'est plus proportionnelle à la distance, et les oscillations ne sont plus symétriques par rapport à la position d'équilibre.
La nouvelle valeur du potentiel portée dans l'équation de Schrödinger donne les niveaux d'énergie corrigés. Ces niveaux sont donnés par un développement en série de la forme : Eυ = hv(υ + 1/2) – hvxe(υ + 1/2)2 + hvye(υ + 1/2)3 + ... xe est une constante petite : les termes suivants, en puissance croissante de (υ + 1/2) où s'introduisent des constantes analogues ye, ze, ... de plus en plus petites deviennent rapidement négligeables. En pratique, les deux premiers termes suffisent à représenter les résultats expérimentaux avec une précision acceptable. L'expression qui donne la valeur en cm–1 des niveaux d'énergie est appelée terme spectral, noté G(υ) :
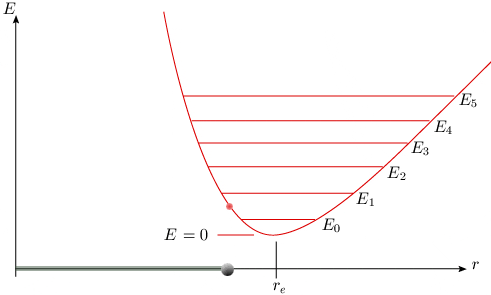
Le diagramme de niveaux d'énergie de l'oscillateur anharmonique est donc composé d'une série de lignes qui ne sont pas tout à fait équidistantes. L'intervalle entre les lignes décroît progressivement d'une petite quantité chaque fois que l'on passe d'un niveau à un niveau supérieur. La quantité ωexe est appelée constante d'anharmonicité, et le terme qui la contient est nommé correction d'anharmonicité. Le tableau 2.4 donne des valeurs des constantes de force et d'anharmonicité pour quelques molécules. Les valeurs données pour les molécules homonucléaires ne sont pas déterminées par absorption infrarouge mais par les spectres électroniques (voir module 5). Tableau 2.4 Constantes de vibration pour quelques molécules.
Énergie du niveau zéro Le niveau énergétique vibrationnel le plus bas que la molécule peut atteindre est celui qui correspond à υ = 0. D'après l'équation 2.10, l'énergie E0 correspondante, soit :
n'est pas nulle. Autrement dit, il est impossible que la molécule s'arrête complètement de vibrer. Même dans l'état énergétique le plus bas, la molécule possédera toujours un peu d'énergie de vibration. Ce niveau d'énergie minimum est appelé point d'énergie zéro.
Expression mathématique de la courbe de potentiel complète Lorsqu'on s'écarte trop du minimum, c'est-à-dire pour des nombres quantiques élevés, la correction cubique n'est plus satisfaisante; pour de grandes valeurs de la distance internucléaire, cette courbe de potentiel atteint non pas une asymptote, mais un maximum suivi d'une décroissance. Plusieurs formules théoriques ont été proposées pour représenter de manière plus adéquate la courbe de potentiel. La plus utilisée est la formule de Morse :
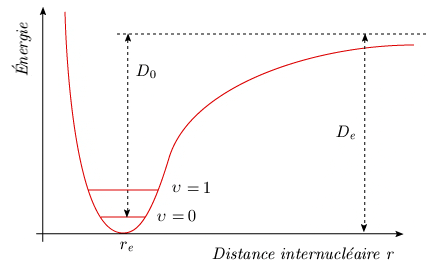
La courbe est représentée à la figure 2.7. De est l'énergie de dissociation spectroscopique, soit l'intervalle compris entre le minimum et la valeur asymptotique de l'énergie aux grandes distances internucléaires. À cause de l'énergie non nulle du niveau fondamental υ = 0, cette énergie est plus grande que l'énergie nécessaire pour briser une molécule, appelée énergie de dissociation chimique (ou énergie de liaison), notée D0.
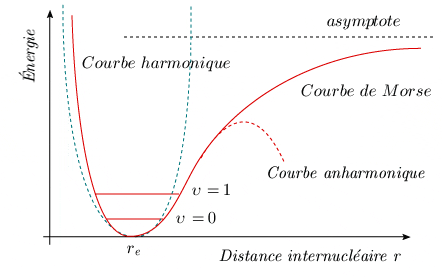
La figure 2.8 compare, sur un même graphique, la courbe parabolique de base de l'oscillateur harmonique, la courbe anharmonique, qui inclut la correction cubique, et la courbe de Morse.
Signification physique de la théorie quantique Matérialisons la courbe d'énergie potentielle par un tube de même forme dans lequel circule sans frottement une bille d'acier. Cette bille assimilée à un point matériel possède, du fait du champ gravitationnel, une énergie potentielle qui varie de la même manière que celle de la molécule. Son mouvement (tout au moins du point de vue énergétique) représente le mouvement de la molécule. La condition quantique implique que la bille part de hauteurs bien déterminées au-dessus du minimum d'énergie potentielle. Si on lâche la bille à partir d'un certain niveau énergétique, elle passera par le minimum de la courbe pour remonter au même niveau (puisqu'il n'y a pas de frottement), puis exécutera des oscillations en reproduisant le même mouvement. La molécule fera de même si on écarte les deux atomes : elle repassera par un état où la distance internucléaire est re pour aller jusqu'à un état où la distance internucléaire est plus faible. Cet état correspondra à la même énergie potentielle qu'au départ. Ensuite, elle oscillera entre ces deux positions extrêmes. On voit, par analogie avec le mouvement de la bille, que les oscillations ne sont pas symétriques. La molécule passe plus de temps à décrire la demi-oscillation correspondant à une élongation que la demi-oscillation correspondant à une contraction. Mentionnons également que la description quantique du mouvement de l'oscillateur harmonique remet en question non seulement le caractère continu des valeurs d'énergie possibles, mais aussi la nature même de ce mouvement. Ainsi, la mécanique quantique prévoit, du moins pour de petits nombres quantiques, que les positions extrêmes sont moins probables que les positions situées près de l'équilibre, alors que le modèle classique prévoit exactement le contraire. En effet, selon le modèle classique, l'oscillateur se déplace plus lentement quand il se trouve loin de la position d'équilibre; il passe donc une plus grande partie de son temps dans ces régions. En conséquence, à un instant quelconque, il y a plus de chances de le trouver loin de la position d'équilibre que près de celle-ci. Toutefois, en dépit de ses limitations, le modèle classique (ou semi-quantique, quand on lui associe la quantification des énergies possibles) demeure utile pour se représenter et comprendre bon nombre des caractéristiques du mouvement des molécules.
Spectres d'absorption de l'oscillateur anharmonique Les règles de sélection sont un peu modifiées par rapport au modèle simple précédent. On trouve que si la transition Δυ= ± 1 se produit toujours avec une grande probabilité, les transitions Δυ = ±2, ±3, etc. peuvent également se produire, mais avec une probabilité beaucoup plus faible. Les fréquences des raies correspondant à ces transitions peuvent être facilement trouvées :
De façon générale, on a :
Si l'on pose b = ωe – ωexe et c = ωexe, on peut récrire l'équation 2.13 de la façon suivante :
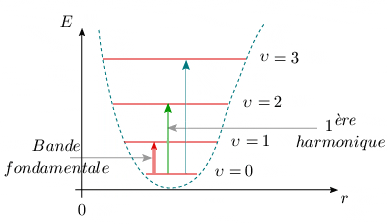
Cette dernière formule est tout à fait analogue à la formule empirique 2.2. Par ailleurs, la faible probabilité des transitions Δυ = 2, 3 ... (figure 2.9) peut être reliée à la décroissance rapide de l'intensité des diverses harmoniques du spectre d'absorption (figure 2.3). Cette question est abordée plus en détails au module 5.
Constantes moléculaires déterminées à partir des constantes de vibration
Les constantes théoriques d'harmonicité ωe et d'anharmonicité ωexe peuvent être déterminées expérimentalement en comparant l'équation 2.10 et l'équation 2.2. La constante ωe est liée à la fréquence vraie de vibration de la molécule, donc à la constante de force réelle k du mouvement (équation 2.7). Par contre, la constante ωexe n'est liée directement à aucune grandeur fondamentale de la molécule, mais elle est d'extrême importance pour fixer les positions relatives des niveaux. La connaissance précise de ces positions permet, par extrapolation, de déterminer l'énergie de dissociation. Les spectres de vibration sont difficiles à observer expérimentalement pour des nombres quantiques υ élevés. Aussi, un petit nombre de niveaux (en général 2 ou 3) peut être déterminé, ce qui est très insuffisant pour obtenir une valeur précise de ωe et ωexe. On observe un nombre de niveaux beaucoup plus grand dans les spectres électroniques, qui font l'objet du module 5, et on obtient de ce fait des valeurs acceptables des constantes. Voici cependant dès maintenant une méthode approximative, appelée méthode de Birge-Spooner, qui permet de calculer l'énergie de dissociation à partir des valeurs de ωe et ωexe déterminées expérimentalement. Le terme spectral G (υ) représente l'énergie des niveaux mesurée en cm–1. Nous admettrons que les niveaux se rapprochent de plus en plus et que, à la limite, la différence entre deux niveaux tend vers zéro lorsque ceux-ci atteignent la valeur de l'énergie de dissociation De. Il en résulte qu'à la limite, c'est-à-dire au voisinage de l'énergie de dissociation, on a : ΔG = G(υ + 1) – G(υ) = 0 Calculons d'abord, à l'aide de l'équation 2.10, l'expression de ΔG en fonction de v : G(υ + 1) = ωe (υ + 3/2) – ωexe (υ + 3/2)2 G(υ) = ωe (υ + 1/2) – ωexe (υ + 1/2)2 ΔG = G(υ + 1) – G(υ) = ωe – 2 ωexeυ – 2 ωexe En admettant que xe « 1, ce qui entraîne ωe >> ωexe, il vient que : ΔG ≅ ωe – 2 ωexeυ et donc que ΔG = 0 lorsque :
Cette expression pour la valeur maximum de υ permet de calculer De. En effet, en la substituant à υ dans l'équation 2.10, on obtient, après quelques manipulations algébriques :
ce qui peut s'écrire comme suit :
Mais comme ωexe est négligeable devant ωe, on peut négliger le second terme entre crochets, de sorte qu'on obtient l'expression simple suivante, appelée formule de Birge-Spooner :
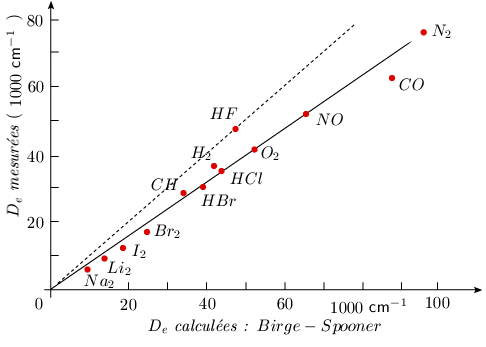
Les valeurs obtenues par la formule de Birge-Spooner sont relativement proches des valeurs tirées de l'expérimentation. En fait elles sont souvent légèrement supérieures (~ 20 %) aux valeurs expérimentales. La figure 2.10 montre, pour quelques molécules, la corrélation entre les valeurs expérimentales et les valeurs ainsi calculées. Sur cette figure, la droite pointillée correspond à l'identité entre les valeurs calculées par la méthode de Birge-Spooner et celles mesurées à l'aide de la thermochimie. Si le point représentatif de HF se place sur cette droite, toutes les autres valeurs calculées sont en dessous de cette droite pointillée.
Rappelons enfin l'intérêt de la méthode qui indique la valeur du nombre quantique de vibration au voisinage de l'asymptote (limite de dissociation).
Conclusions La mécanique classique est insuffisante pour l'interprétation des observations spectroscopiques du mouvement de vibration des molécules diatomiques. Par contre, elle permet de mieux comprendre l'application de la mécanique quantique. D'après la mécanique quantique, les molécules diatomiques ne peuvent vibrer que selon des niveaux d'énergie quantifiés associés à des nombres quantiques de vibration. De plus, des règles de sélection précisent les transitions acceptables entre ces niveaux. Par ailleurs, l'interprétation du spectre observé dans le proche infrarouge permet d'obtenir la fréquence de vibration de la molécule, la constante de force de la liaison, de même qu'une très bonne approximation de l'énergie de rupture de cette liaison (ou de dissociation de la molécule). Fait à noter, même à la température du zéro absolu, soit 0 K, la molécule vibre toujours.
Pour en savoir plus Liens utiles Une base de données, appelée
WebBook, contenant, entre autres, les valeurs des constantes
moléculaires (incluant les constantes de rotation
B et D) des molécules diatomiques, est
disponible sur le site du National Institute of
Standards and Technology (NIST). On peut y faire une
recherche par nom de molécule, ou encore à
partir d'une liste de 400 molécules diatomiques,
tirée des travaux de Huber et Herzberg. Valeur des constantes de rotation : http://webbook.nist.gov/chemistry/name-ser |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||