|
|
MODULE 2 Vibration
des molécules diatomiques
Problèmes
- Une solution de CO dans le tétrachlorure de
carbone montre une bande d'absorption vers
2 140 cm–1.
Calculez la constante de force de la liaison CO,
k, en dynes/cm. Corrigé
- Les valeurs de ωe, ωexe
(en cm-1) et de re pour
H2, HD et D2 sont les suivantes
:
|
Molécules
|
ωe (cm–1)
|
ωexe
(cm–1)
|
re (nm)
|
|
H2
|
4401,21
|
121,33
|
0,074
|
|
HD
|
3813,1
|
91,65
|
id.
|
|
D2
|
3115,5
|
61,82
|
id.
|
- Calculez l'énergie du point zéro
pour chaque molécule en unités SI.
- Calculez l'énergie de dissociation de
chaque molécule; commentez.
Corrigé
- La molécule excitée XeF* (état B
2π1/2) présente un
spectre vibrationnel tel que :
ωe
= 308,6 cm–1
et ωe
xe = 1,52 cm–1
Calculez l'énergie de dissociation
de cette molécule en cm–1,
cal/mol et J/mol. Corrigé
- La bande fondamentale ν1 de CO
est située à 2143,3 cm–1
et la première harmonique 2ν1
à 4259,7 cm–1.
- Calculez ωeωexe,
la constante de force de la liaison et le nombre de
vibrations par seconde.
- Évaluez l'énergie de dissociation
spectroscopique de la molécule.
- Quelle est l'énergie du point zéro
de la molécule?
- Dans un état électronique de CO, on
observe des valeurs ωe' et ωexe'
égales à 1518,24 et 19,4 cm–1.
Calculez l'énergie de dissociation de cet
état électronique excité.
- Dessinez sur le même graphe, E =
f (rC–O), ce que
pourraient être les deux courbes de Morse.
Corrigé
- Un oxyde diatomique a une énergie de vibration
située à 1 876 cm–1
et une constante de force de
1 550 N×m–1. Identifiez
la molécule. Corrigé
- La molécule DCl présente les
caractéristiques vibrationnelles suivantes
(exprimées en cm–1) :
ωe = 2 145,163 ωexe = 27,1825 et
ωeye
= 0,086 49
Calculez les énergies en cm–1
des 11 premiers niveaux d’énergie de
vibration dans l’hypothèse des modèles
harmonique et anharmonique ainsi que dans le cas de la
correction du terme cubique. En déduire
l’importance relative de la correction due à
l’anharmonicité par rapport au modèle
harmonique ainsi que celle due à
l’introduction du terme cubique par rapport au
modèle anharmonique. Concluez. Corrigé
-
En spectroscopie électronique (voir
module 5),
on mesure les constantes B, notées
Bυ dans divers niveaux υ
de l'état électronique fondamental de la
molécule d'oxygène. Calculez, à
partir des valeurs apparaissant dans le tableau suivant,
la longueur de la liaison de la molécule dans
chacun des niveaux υ
mentionnés.
|
υ
|
Bυ (cm–1)
|
υ
|
Bυ (cm–1)
|
|
0
|
1,43767
|
4
|
1,37492
|
|
1
|
1,42183
|
5
|
1,35942
|
|
2
|
1,40610
|
6
|
1,34396
|
|
3
|
1,39047
|
7
|
1,32851
|
Problèmes avec VR
Molécules
-
Placez VR Molécules à la
page 1.
À l'aide de la grille, dont
l'intensité peut être ajustée au
moyen du curseur situé en haut et à droite
de la fenêtre, déterminez le rapport des
amplitudes des oscillations des deux atomes. Comparez la
valeur de ce rapport avec celui des masses des atomes, en
tenant compte de l'incertitude sur vos mesures.
Pour vous faciliter la tâche, vous pouvez modifier
le niveau de zoom, l'amplitude du mouvement ainsi que la
vitesse de la simulation à l'aide des boutons ou
curseurs appropriés situés dans la partie
droite de la fenêtre. N'hésitez pas non plus
à déplacer la molécule, en
cliquant-déplaçant un de ses
atomes. Corrigé
-
Placez VR Molécules à la
page 9.
Remarquez la lettre A à gauche du nom de la
molécule, qui indique que la correction
d'anharmonicité est activée.
Le déplacement de l'atome d'hydrogène de
part et d'autre de son point d'équilibre vous
paraît-il symétrique dans le niveau
fondamental? Dans le niveau maximal prévu dans VR
Molécules? En vous aidant de la grille, chiffrez
approximativement le rapport de ces déplacements
pour ces deux niveaux.
Répétez les mêmes calculs pour la
molécule CO de la page 1.
Comment ce résultat se compare-t-il avec le
précédent? N'oubliez pas d'activer
l'anharmonicité, à partir de la
fenêtre qui s'ouvre quand on clique sur le bouton ΔE
situé au-dessus des curseurs de
vibration-rotation. Corrigé
-
Placez VR Molécules à la
page 10
qui présente (en deux exemplaires) la
molécule de D2, soit une
molécule d'hydrogène où les atomes
ont été remplacés par leur isotope
de masse 2, le deutérium. Celui-ci possède
un neutron excédentaire, représenté
par le point noir au centre de l'atome.
En faisant varier l'énergie de vibration et en
activant si nécessaire la correction
d'énergie appropriée, déterminez les
valeurs des constantes ωe et ωexe
pour cette molécule. Corrigé
Corrigés
-
Voir le site http://www.univ-tln.fr/~gfev/Spectro/09Spectro.html
-
L'énergie du niveau fondamental ou
l'énergie du point zéro est donnée
par la relation :
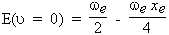
|
Molécule
|
E (υ = 0)
(cm–1)
|
E (υ = 0)
(kJ/mol)
|
De (cm–1)
|
|
H2
|
2 170,27
|
25,95
|
39 913,1
|
|
HD
|
1 883,6
|
22,54
|
39 661
|
|
D2
|
1 542,3
|
18,45
|
39 242
|
Exemple de calcul :
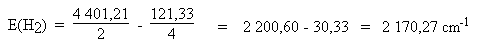
Pour convertir ces valeurs on peut
appliquer la formule suivante, en n'oubliant pas de
multiplier par le nombre d'Avogadro et en introduisant un
facteur 100 pour ramener les cm–1 en
m–1, une unité de base du
système SI.
E
= hc N N
= 6,626 176 10–34 ×
2,997 924 108 × 2
170,27 × 100 × 6,022 05
1023
E = 25
953,4 J/mol
Vérifions la cohérence des
unités.
E
= hc N N
[J ·
s] [m · s–1
] [cm–1] [cm
· m–1 ] [mol–1]
= [J · mol–1]
L'énergie de dissociation
spectroscopique est établie par la formule de
Birge-Spooner :
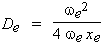
et l'énergie de dissociation
chimique est reliée à celle-ci
par :
D0 = De – E (υ = 0)
On obtient les valeurs
suivantes :
|
Molécule
|
De (cm–1)
|
D0 (cm–1)
|
|
H2
|
39 913,1
|
37 742,9
|
|
HD
|
39 661
|
37 777
|
|
D2
|
39 242
|
37 700
|
On voit que la substitution isotopique de
la molécule d'hydrogène par le
deutérium n'a que peu d'influence sur la valeur de
l'énergie de dissociation spectroscopique
De, et une influence négligeable
sur celle de l’énergie de dissociation
chimique D0.
-
L'énergie de dissociation
spectroscopique est établie par la formule de
Birge-Spooner :
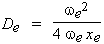
D'où, en remplaçant par les
valeurs appropriées :
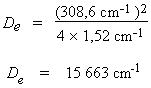
On ne demandait pas spécifiquement
de faire la différence entre l'énergie de
dissociation spectroscopique et l'énergie de
dissociation chimique. Si cela avait été le
cas, il aurait fallu soustraire de De
l'énergie du niveau fondamental (υ = 0)
pour obtenir l'énergie de dissociation chimique
D0.
L'énergie du niveau fondamental ou
l'énergie du point zéro est donnée
par la relation :
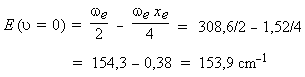
Ce qui donne pour l'énergie de
dissociation chimique :
D0 = 15 509 cm–1
Pour convertir ces valeurs en cal/mol et
en J/mol on applique la même règle
qu'à l'exercice précédent :
E
= hc N N
E = 6,626 176 10–34
× 2,997 924 × 108
×  × 6,022 05 × 1023 × 6,022 05 × 1023
E = 1 873,1 J/mol
Pour transformer des joules en calories,
il suffit de diviser par 4,18 :
De = 0,448
kcal/mol
-
- L'énergie d'un niveau de vibration
υ est donnée par la relation :
E /
hc = G(υ) =
ωe (υ + 1/2) – ωexe
(υ + 1/2)2
La différence d'énergie
entre un niveau quelconque et le niveau fondamental
est donc :
G(υ) –
G(0) = ωe (υ
+ 1/2) – ωe
xe (υ + 1/2)2
– ωe (1/2) + ωexe
(1/2)2
G(υ) –
G(0) = ωeυ
– ωexe υ2
– ωexe υ
Dans le cas où υ
= 1, on obtient :
G(1) –
G(0) = ωe – ωexe
– ωexe =
ωe – 2 ωexe
Dans le cas où υ
= 2, on obtient :
G(1) –
G(0) = 2 ωe
– 4 ωexe
– 2 ωexe = 2 ωe
– 6 ωexe
On peut donc écrire :
ωe –
2 ωexe
= 2 143,3 cm–1
et 2 ωe – 6
ωexe =
4 259,7 cm–1
En soustrayant deux fois la
première relation de la seconde, on obtient
:
2 ωe –
6 ωexe
= 4 259,7 cm–1
– 2 [ωe
– 2 ωexe
= 2 143,3 cm–1]
– 2 ωexe
= – 26,9 cm–1
et ωexe
= 13,45 cm–1
En remplaçant cette
dernière valeur dans l'une ou l'autre des
équations précédentes, on obtient
la valeur de ωe :
ωexe
= 2 170,2 cm–1
La relation entre l'énergie
exprimée en cm–1 et la
fréquence est donnée par la relation
:
 = v/c d'où
ν = c = v/c d'où
ν = c
Donc :
ν =
c = (2,9979
1010 cm/s) × (2143,3 cm–1)
= 6,425 1013 s–1 = (2,9979
1010 cm/s) × (2143,3 cm–1)
= 6,425 1013 s–1
Le nombre d'oscillations par seconde
est justement égal à cette
fréquence.
Pour un oscillateur mécanique,
la constante de force, k, est donnée par
la relation :
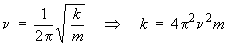
où ν est la
fréquence et m la masse de
l'oscillateur. Pour le vibrateur C–O, on peut
confondre les deux fréquences, celle de
l'oscillateur mécanique et celle de la
molécule C–O. Par contre, on doit
remplacer m par la masse réduite de la
molécule μ. En SI, on
obtient :
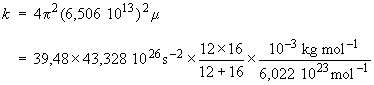
k
= 39,48 × 42,328 × 6,857 /
6,022 = 1 903 kg s–2
k = 1 903 N
- L'énergie de dissociation spectroscopique
est donnée par la formule de Birge-Spooner :
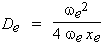
D'où, en remplaçant par
les valeurs, on obtient :
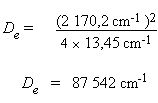
Transformation de cette valeur en
kJ/mol :
 = v/c d'où
ν = c = v/c d'où
ν = c
E = hν
= hc
E = 6,6262 10–34
J s × 2,9979 1010 cm/s × 87 542
cm–1
= 1,739 × 10–18 J
Cette énergie correspond
à l'énergie d'une molécule. Pour
une mole, on obtient :
E
= 1,739 10–18 J ×
6,022 05 1023 =
10,472 105 J
E = 1 047,2 kJ/mol
Ou encore :
E
= 1 047,2 / 4,18 =
261,1 kcal/mol
- L'énergie du point zéro de la
molécule s'obtient en utilisant la
formule :
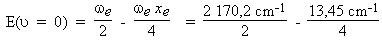
E (υ
= 0) = 1 081,7 cm–1
En unités plus conventionnelles
et par mole, on obtient :
E0 =
12,936 kJ/mol ou encore 3,095 kcal/mol
- L'énergie de dissociation de l'état
électronique excité se calcule de la
même façon que
précédemment :
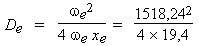
De
= 29 704,3 cm–1
- On demande de mettre sur un graphe E =
f (rC–O) les deux
courbes de Morse, celle correspondant à
l'état fondamental et celle relative à
l'état électronique excité. On ne
connaît que peu de choses pour chacune de ces
courbes, sinon qu'elles ont une asymptote verticale
dans leur branche de gauche et une asymptote
horizontale pour r tendant vers l'infini. On
connaît aussi les énergies de
dissociation spectroscopique des deux états
électroniques. Par conséquent, on sait
situer chacune des deux asymptotes horizontales par
rapport au minimum de deux courbes de Morse. Dernier
élément, la courbe de Morse de
l'état excité ne peut pas se retrouver
à des énergies inférieures
à celle de l'état fondamental. La
position la plus «basse», la moins
énergétique pour l'état
excité, est donc celle où les deux
asymptotes horizontales sont confondues. Aucun
élément ne vient préciser
davantage ce point. Il en est de même de la
position relative des deux minima, positions
exprimées en terme de distance C–O.
-
La fréquence d'un oscillateur est
donnée par la relation :
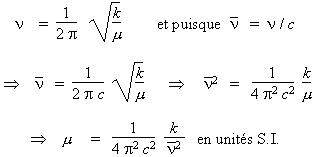
Pour la molécule X–O :
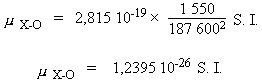
Comme :
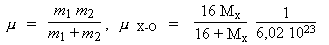
Mx est la masse de
l'atome inconnu.
On a :
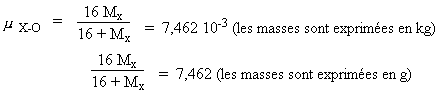
D'où :
16
Mx =
7,462 (16 + Mx) = 16
× 7,462 + 7,462 Mx
8,538 Mx
= 119,389
Mx =
13,983
Soit Mx ≅ 14.
Il s'agit donc de l'atome d'azote et donc de la
molécule NO.
-
Il s’agit simplement
d’appliquer, pour chacun des niveaux de vibration
υ = 0 à υ = 10, la
formule apparaissant dans le module :
E = hν
(υ + 1/2) – hνxe
(υ + 1/2)2 + hνye
(υ + 1/2)3 + ...
Ou encore :
E = ωe
(υ +1/2) – ωexe
(υ + 1/2)2 + ωeye
(υ + 1/2)3 + ...
Un outil comme Excel est tout à
fait approprié pour faire ce travail. On obtient
le tableau qui suit.
|
Vibration harmonique
|
Correction
pour l'anharmonicité
|
Vibration
anharmonique
|
Correction
pour le terme cubique
|
Vibration
cubique
|
|
ωe(υ +
1/2)
(cm–1)
|
ωexe(υ+1/2)2
(cm–1)
|
Énergie
(cm–1)
|
Correction
(%)
|
ωeye(υ+1/2)3
(cm–1)
|
Énergie
(cm–1)
|
Correction
(%)
|
|
1072,5815
|
–6,7956
|
1065,7859
|
–0,63
|
0,0108
|
1065,7967
|
0,00
|
|
3217,7445
|
–61,1606
|
3156,5839
|
–1,90
|
0,2919
|
3156,8758
|
0,01
|
|
5362,9075
|
–169,8906
|
5193,0169
|
–3,17
|
1,3514
|
5194,3683
|
0,03
|
|
7508,0705
|
–332,9856
|
7175,0849
|
–4,44
|
3,7083
|
7178,7931
|
0,05
|
|
9653,2335
|
–550,4456
|
9102,7879
|
–5,70
|
7,8814
|
9110,6693
|
0,09
|
|
11798,3965
|
–822,2706
|
10976,1259
|
–6,97
|
14,3898
|
10990,5156
|
0,13
|
|
13943,5595
|
–1148,4606
|
12795,0989
|
–8,24
|
23,7523
|
12818,8512
|
0,19
|
|
16088,7225
|
–1529,0156
|
14559,7069
|
–9,50
|
36,4880
|
14596,1948
|
0,25
|
|
18233,8855
|
–1963,9356
|
16269,9499
|
–10,77
|
53,1157
|
16323,0655
|
0,33
|
|
20379,0485
|
–2453,2206
|
17925,8279
|
–12,04
|
74,1544
|
17999,9822
|
0,41
|
|
22524,2115
|
–2996,8706
|
19527,3409
|
–13,31
|
100,1230
|
19627,4639
|
0,51
|
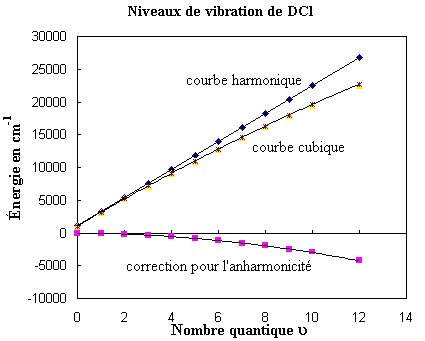
Les résultats montrent que
l’anharmonicité introduit une correction
importante à l’énergie du niveau υ.
En effet, si cette correction n’est que de – 0,63 %
pour le niveau υ = 0, elle atteint – 13,3 %
pour le niveau υ = 10. L’ajout
d’un terme cubique a un effet beaucoup moindre. La
dernière colonne de ce tableau montre que la
correction dépasse à peine 0,5 % pour le
niveau υ = 10. Ce pourcentage de
correction, faut-il le rappeler, est calculé par
rapport aux résultats du modèle
anharmonique.
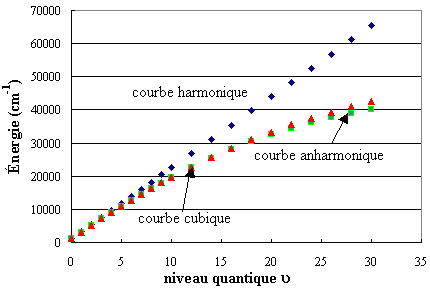
Les mêmes résultats peuvent
être représentés graphiquement. Le
graphique suivant montre la variable énergie
exprimée en cm–1 en fonction du
nombre quantique u.
On a représenté seulement
trois courbes :
- La courbe relative à l’énergie
des niveaux selon le modèle harmonique : la
dépendance de l’énergie sur le
nombre quantique υ est
linéaire;
- La courbe représentant la correction due
à l’anharmonicité, et;
- La courbe relative à l’énergie
des niveaux selon le modèle anharmonique : la
dépendance de l’énergie sur le
nombre quantique υ est
quadratique.
La correction due à
l'anharmonicité peut être
négligée tant que le nombre quantique de
vibration ne dépasse pas la valeur 4. Au-dessus de
cette valeur, la correction n'est plus négligeable
: elle est supérieure à 4 %. Par
contre, la correction du terme cubique demeure
négligeable. On n'a pas représenté
les courbes correspondant à la correction du terme
cubique. Il en aurait été de même
avec la courbe représentant l’énergie
des niveaux dans le cas du modèle cubique, qui
aurait été confondue avec la courbe du
modèle anharmonique. Cette similitude des deux
courbes apparaît dans la figure suivante où
même avec un nombre quantique de 25, la
différence entre les deux courbes demeure
limitée : de l'ordre de 4 %.

Autre représentation des
mêmes courbes sur une échelle plus large du
nombre quantique de vibration.
-
La démarche en est une de
comparaison entre, d’une part, la valeur chimique de
l’énergie de dissociation d’une
molécule diatomique et, d’autre part, la
même valeur calculée à partir des
constantes vibrationnelles de la même
molécule. On fera la comparaison des
énergies en unités de cm–1.
La première étape consiste donc à
transformer les kilojoules en cm–1.
E =
hc = 6,6262 10–34 J s ×
2,997 924 10–10 cm/s × 1 cm–1
= 6,6262 10–34 J s ×
2,997 924 10–10 cm/s × 1 cm–1
E =
19,8648 10–24 J pour 1 cm–1
Comme ce sont là des grandeurs
moléculaires, il faut multiplier par le nombre
d’Avogadro pour obtenir les grandeurs molaires :
E = 19,8648 10–24
J × 6,022 1023 mole –1
pour 1 cm–1
E = 119,63 10–1
J/mol pour 1 cm–1
L’énergie de la liaison H–H,
en cm–1, devient donc :
E (H–H)
= 436 000 J / 11,963 J × 1 cm–1
E (H–H)
= 36 459 cm –1
L’énergie de la liaison peut
être calculée théoriquement à
partir des constantes vibrationnelles :
D0
(spectroscopique) = De –
l’énergie du point zéro
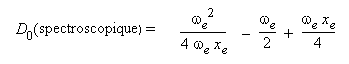
En remplaçant les valeurs de ωe
et de ωexe, on obtient
pour l’hydrogène :
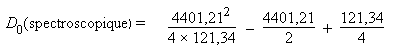
D0
(spectroscopique) = 39 908,8 – 2
200,6 + 30,3 = 37 739,5 cm
–1
Cette valeur est un peu plus
élevée (3,5 %) que la valeur obtenue
par voie expérimentale. Les autres valeurs sont
calculées de la même manière et
apparaissent dans le tableau qui suit.
|
Molécule
|
D0 (expérimental)
(cm–1)
|
D0 (spectroscopique)
(cm–1)
|
Écart
(%)
|
|
H–H
|
36 459
|
37 739,5
|
+3,5
|
|
H–F
|
47 079
|
47 588,9
|
+ 1,1
|
|
H–Cl
|
36 124
|
40 858,6
|
+ 13,1
|
|
H–I
|
24 985
|
32 480
|
+ 30,0
|
|
I–I
|
12 618
|
18 856,6
|
+ 48,9
|
|
Cl–Cl
|
27 408
|
29 052,7
|
+ 6,0
|
|
N=N
|
79 051
|
95 914
|
+ 21,2
|
|
C=O
|
60 500
|
87 483
|
+ 44,5
|
Corrigés des problèmes
avec VR Molécules
-
Le rapport des déplacements des
deux atomes est à peu près égal
à l'inverse du rapport de leurs masses, soit 0,75
(déplacement de O sur déplacement de
C).
-
Avec HCl, on obtient les valeurs suivantes
pour l'atome d'hydrogène :
Pour υ = 0
(valeurs divisées par 5 à cause de
l'amplitude à5×) :
11,6 pm / 10,0 pm = 1,16 ± 0,04;
Pour υ = 5 :
50 pm / 28 pm =
1,8 ± 0,1
Avec CO, on obtient les valeurs suivantes pour l'atome de
carbone :
Pour υ = 0
(amplitude 5×) : 2,8 pm / 2,8 pm
= 1,0 ± 0,1
Pour υ = 5
(amplitude 5×) :
10,8 pm / 7,6 pm =
1,42 ± 0,03
Le rapport des déplacements de part et d'autre du
point d'équilibre, une des conséquences de
l'anharmonicité, est égal ou proche de
l'unité pour le niveau fondamental; à υ = 5,
il vaut 1,4 et 1,8 pour CO et HCl respectivement.
L'anharmonicité est donc plus prononcée
pour HCl.
-
En l'absence d'anharmonicité,
l'énergie du niveau υ est
donnée, en unités de nombre d'onde, par
l'équation 2.10 sans le terme en (υ+1/2)2 :
G(υ) ≅ ωe
(υ + 1/2)
La valeur de ωe
peut donc être déterminée à
partir de celle de l'énergie pour un niveau υ
quelconque. Pour un maximum de précision,
choisissons le niveau υ = 5; on
trouve alors :
ωe
= G(5) / 5,5 = 17
140 / 5,5 = 3120 cm–1
Pour déterminer la valeur de la
constante ωexe, il
faut activer la correction d'anharmonicité pour la
molécule de gauche. Si la valeur de la constante
ωe est connue, une seule valeur
d'énergie est requise pour déterminer la
valeur de ωexe.
D'après l'équation 2.10
complète, on a en effet :
ωexe
(υ+1/2)2 = ωe
(υ+1/2) – G(υ)
où G(υ) est
la valeur incluant la correction et ωe
(υ+1/2) la valeur sans correction. On
obtient, toujours en considérant υ = 5 :
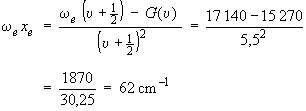
|



