MODULE 3  Vibration-rotation des molécules diatomiques

Problèmes

1. Le spectre de rotation-vibration de l'oxyde de carbone comporte dans le proche infrarouge une bande intense dans la région de 2100-2200 cm^–1. Avec un appareil de basse résolution on obtient la série de raies suivantes : 2124, 2128, 2132, 2136, 2140, 2148, 2152, 2156, 2160 cm^–1.

   1. Déterminez le moment d'inertie, la distance internucléaire et la fréquence de vibration de la molécule CO.
      
      
   2. Déterminez la valeur de la constante de distorsion centrifuge de la même molécule.

   Corrigé

2. La fréquence fondamentale de l'élongation O-H dans le méthanol est située à 3300 cm^–1. Prédisez la position de la bande correspondante pour l'espèce isotopique CH₃OD.

   Note : Il n'y a pas de corrigés pour ce problème, ainsi que pour les problèmes 3 à 5.

3. Le spectre infrarouge de H³⁵Cl sous haute résolution montre des raies d'absorption dont les fréquences sont indiquées dans le tableau qui suit. En utilisant un logiciel (ordinateur, micro-ordinateur ou calculatrice appropriée), calculez au moyen d'une régression linéaire ou d'un moindre carré les coefficients du polynôme suivant : E  =  b + am + cm² + dm³, où E est l'énergie de la raie et m un nombre entier.

   Établissez au préalable la valeur de m pour chaque raie (colonne 3 du tableau suivant). Déduisez-en :

   • l'énergie de la raie manquante;
   • la valeur de ω_e – 2 ω_ex_e;
   • les constantes B (υ = 0) et B′ (υ = 1);
   • la constante de distorsion centrifuge D.

   Tracez les courbes E (cm^–1) = f (J) et E (cm^–1) = f (m) sur le même graphe.

   Spectre de rotation-vibration de H³⁵Cl.

   J	Énergie (cm–1)	m	ΔE (cm–1)	Δ(ΔE) (cm–1)
   10	3072,8558
   			13,5338
   9	3059,3220			-0,7244
   			14,2582
   8	3045,0638			-0,7132
   			14,9714
   7	3030,0924			-0,7036
   			15,6750
   6	3014,4174			-0,6971
   			16,3721
   5	2998,0453			-0,6598
   			17,0319
   4	2981,0134			-0,6912
   			17,7231
   3	2963,2903			-0,6461
   			18,3692
   2	2944,9211			-0,6493
   			19,0185
   1	2925,9026			-0,6300
   			19,6485
   0	2906,2541			--
   -
   1	2865,1047
   			21,4745
   2	2843,6302			-0,5816
   			22,0561
   3	2821,5741			-0,5694
   			22,6255
   4	2798,9486			-0,5565
   			23,1880
   5	2775,7666			-0,5445
   			23,7265
   6	2752,0401			-0,5288
   			24,2553
   7	2727,7848			-0,5170
   			24,7723
   8	2703,0125			-0,5041
   			25,2764
   9	2677,7361
   Données aimablement transmises par le prof. R. Colin, chimie-physique moléculaire Université Libre de Bruxelles, Bruxelles.

4. Répétez le même problème pour HBr, à partir de la liste suivante des énergies des raies (en cm^–1).

   2 371,71	2 471,13	2 575,52	2 650,08
   2 392,50	2 489,66	2 591,33	2 663,63
   2 412,83	2 507,73	2 606,70	2 676,74
   2 432,72	2 525,36	2 621,61	2 689,39
   2 452,15	2 542,53	2 636,07	2 701,59

5. Répétez le même problème pour H³⁷Cl.

   2 675,9584	2 796,9750	2 923,7377	3 012,1328
   2 701,1927	2 819,5661	2 942,7279	3 027,7879
   2 725,9250	2 841,5877	2 961,0732	3 042,7419
   2 750,1418	2 863,0289	2 978,7650	3 056,9840
   2 773,8293	2 904,1162	2 995,7878	3 070,5036

6. Le spectre infrarouge de DCl sous haute résolution montre des raies d'absorption dont les fréquences sont indiquées dans le tableau ci-dessous. En vous servant des intensités mesurées des raies, départagez les raies appartenant à D³⁵Cl et celles appartenant à D³⁷Cl. En vous inspirant du problème 3 relatif à H³⁵Cl, calculez au moyen d'une régression linéaire ou d'un moindre carré, et cela pour chacune des deux molécules isotopiques, les coefficients du polynôme suivant : E  =  b + am + cm² + dm³, où E est l'énergie de la raie et m un nombre entier.

   Établissez au préalable les valeurs de J et m pour chaque raie. Déduisez-en, pour D³⁵Cl et D³⁷Cl :

   • l'énergie de la raie manquante;
     
     
   • la valeur de ω_e – 2 ω_ex_e;
     
     
   • les constantes B (υ = 0) et B′ (υ = 1), ainsi que les longueurs de liaison correspondantes;
     
     
   • la constante de distorsion centrifuge D.

   Tracez les courbes E (cm^–1) = f (J) et E (cm^–1) = f (m) sur le même graphe. Corrigé

   Spectre de rotation-vibration de DCl : raies observées (υ = 0 → υ = 1).

   nº	Énergie (cm–1)	Absorbance	nº	Énergie (cm–1)	Absorbance
   1	2230,8479	0,043	31	2080,2753	1,096
   2	2224,0387	0,089	32	2077,3076	0,384
   3	2216,9606	0,156	33	2069,2694	1,761
   4	2213,6323	0,049	34	2066,3342	0,686
   5	2209,6132	0,280	35	2058,0468	2,133
   6	2206,3007	0,086	36	2055,1451	0,866
   7	2202,0025	0,455	37	2046,6072	2,224
   8	2198,7071	0,156	38	2043,7399	0,888
   9	2194,1272	0,696	39	2034,9590	2,186
   10	2190,8502	0,243	40	2032,1271	0,875
   11	2185,9952	0,997	41	2023,1001	1,998
   12	2182,7377	0,346	42	2020,3044	0,764
   13	2177,6036	1,360	43	2011,0405	1,761
   14	2174,3672	0,487	44	2008,2814	0,654
   15	2168,9620	1,709	45	1998,7764	1,436
   16	2165,7472	0,638	46	1996,0555	0,521
   17	2160,0666	2,006	47	1986,3186	1,105
   18	2156,8750	0,783	48	1983,6365	0,381
   19	2150,9268	2,201	49	1973,6637	0,785
   20	2147,7596	0,901	50	1971,0211	0,263
   21	2141,5397	2,336	51	1960,8216	0,533
   22	2138,3978	0,984	52	1958,2191	0,173
   23	2131,9144	2,342	53	1947,7905	0,344
   24	2128,7986	1,000	54	1945,2297	0,112
   25	2122,0484	2,221	55	1934,5784	0,198
   26	2118,9605	0,918	56	1932,0590	0,067
   27	2111,9499	1,845	57	1921,1853	0,111
   28	2108,8904	0,713	58	1918,7094	0,036
   29	2101,6186	1,138	59	1907,6167	0,058
   30	2098,5888	0,392	60	1893,8780	0,031
   Données aimablement transmises par le prof. R. Colin, chimie-physique moléculaire Université Libre de Bruxelles, Bruxelles.

7. Mêmes questions pour la transition (υ = 0 → υ = 2). Corrigé

   Spectre de rotation-vibration de DCl : raies observées (υ = 0 → υ = 2).

   nº	Énergie (cm–1)	Absorbance	nº	Énergie (cm–1)	Absorbance
   1	4226,6804	0,056	23	4132,8950	0,047
   2	4221,9699	0,064	24	4117,6476	0,136
   3	4216,7621	0,109	25	4111,8404	0,049
   4	4211,0878	0,162	26	4106,4180	0,245
   5	4210,7603	0,052	27	4100,6380	0,075
   6	4204,9374	0,250	28	4094,7565	0,295
   7	4198,8805	0,091	29	4089,0130	0,104
   8	4198,2980	0,270	30	4082,6384	0,306
   9	4192,2631	0,093	31	4076,9159	0,095
   10	4191,1839	0,331	32	4070,1033	0,287
   11	4185,1716	0,103	33	4064,4441	0,089
   12	4183,6147	0,357	34	4057,1180	0,249
   13	4177,6210	0,1222	35	4051,4871	0,080
   14	4175,5631	0,395	36	4043,7218	0,203
   15	4169,5941	0,123	37	4038,1402	0,072
   16	4167,0576	0,399	38	4029,8939	0,170
   17	4161,1125	0,128	39	4024,3623	0,061
   18	4158,0845	0,352	40	4015,6564	0,121
   19	4152,1627	0,122	41	4010,1606	0,041
   20	4148,6556	0,279	42	4000,9944	0,087
   21	4142,7492	0,092	43	3985,9164	0,061
   22	4138,7699	0,145	44	3970,4534	0,042
   Données aimablement transmises par M. Carleer du laboratoire du prof. R. Colin, chimie-physique moléculaire, Université Libre de Bruxelles, Bruxelles.

8. Pour la molécule DCl, la documentation donne les informations numériques suivantes (en cm^–1) :

   B_e = 5,448 794,    α_e = 0,113 291

   En utilisant la relation qui existe entre la constante de rotation et le niveau de vibration, comparez les valeurs obtenues pour les valeurs de B (υ = 0), B (υ = 1) et B (υ = 2) des deux problèmes précédents. Corrigé

9. Vérifiez graphiquement que B varie comme l'inverse de la distance internucléaire dans le cas de divers états électroniques de l'oxyde de carbone. Déterminez de la même manière, en traçant les graphes appropriés, la dépendance de ω_e avec la distance internucléaire.
   
   Que pouvez-vous dire de la relation, s'il en existe une, entre ω_e et la distance internucléaire? Corrigé

   État électronique	re (pm)	B (cm–1)	ωe (cm–1)
   X 1Σ+	112,83	1,9313	2169,8
   a 3Πr	120,57	1,6912	1743,4
   a′ 3Σ+	135,23	1,3446	1228,6
   d 3Δi	136,96	1,3109	1171,9
   e 3Σ–	138,4	1,2836	1117,7
   A 1Π	123,53	1,6115	1518,2
   I 1Σ–	139,11	1,2705	1092,2
   D 1Δ	139,9	1,257	1094,0
   b 3Σ+	111,3	1,986	2199,3
   Valeurs tirées de http://webbook.nist.gov/chemistry/name-ser.html

10. Pour la molécule C=S, on observe les valeurs suivantes (en cm^–1) : ω_e = 1285,08, B_e = 0,8200 et D_e = 1,43 × 10^–6. Comparez la valeur de ω_e obtenue à l’aide de l’approximation 3.6 avec la valeur expérimentale. Corrigé

Problèmes avec VR Molécules

1. Placez VR Molécules à la page 6. En faisant varier si nécessaire les nombres quantiques, déterminez les valeurs des constantes ω_e, ω_ex_e, B_e et α_e pour la molécule HCl. Corrigé
   
   
2. Placez VR Molécules à la page 7. Vérifiez les relations 3.7, 3.8 et 3.9 pour ces deux variantes de la molécule d'hydrogène. Corrigé
   
   
3. Placez VR Molécules à la page 8. En cliquant sur le nom de la molécule contrôlée, en haut à gauche, sélectionnez une des molécules suivantes : O₂, Cl₂, HF, CO, N₂. Pour la molécule que vous avez choisie, déterminez le plus grand nombre de constantes moléculaires possible. N'oubliez pas d'activer si nécessaire les corrections d'énergie (dans la fenêtre en bas à gauche portant ce nom, qui apparaît ou disparaît quand on clique sur le bouton ΔE situé sous le nom de la molécule.) Corrigé

Corrigés

1. 1. On note que les raies sont également espacées d’une énergie de 4 cm^–1.

      2B  =  4 cm^–1 et B  =  2 cm^–1

      On reconnaît sans difficulté l’absence d’une raie à 2144 cm^–1. Cette raie représente la transition de vibration pure. Cette transition est inexistante à cause de la règle de sélection ΔJ = ±1. Les raies situées à des énergies supérieures font partie des raies riches, R (ΔJ = +1) et celles à plus basses énergies sont appelées les raies pauvres, P (ΔJ = –1).

      Le moment d’inertie de la molécule est obtenu à l’aide de la relation :

      

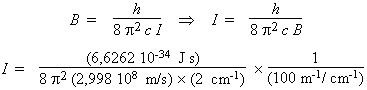
      I  = 14,00 × 10^–47 kg × m²

      

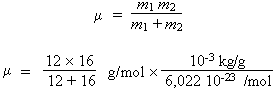
      μ  =  1,1387 10^–26 kg

      Le facteur 10^–3 est introduit pour tenir compte du fait que les masses atomiques sont exprimées en kg/mol et que le rotateur étant bien la molécule, la masse de la molécule est égale à la masse molaire divisée par le nombre d’Avogadro.

      En remplaçant chaque valeur littérale par sa valeur numérique, on obtient :

      

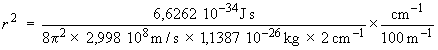
      r²  =  1,229 × 10^–20 m²

      ⇒    r  =  1,109 × 10^–10 m  =  110,9 pm

       

      Notons que ce résultat peut être obtenu plus simplement grâce à la relation r²  =  I / μ.

   2. Les données numériques suggèrent que l'intervalle entre les raies est constant, ce qui laisse entrevoir que la constante de distorsion centrifuge est nulle, ou du moins très faible. Pour obtenir sa valeur, il aurait fallu utiliser un appareil de mesure à grande résolution, de façon à pouvoir mesurer les raies avec une précision de un ou deux ordres de grandeur supérieure. Par ailleurs, l’observation et la mesure de plusieurs autres raies auraient sans doute facilité cette mesure.

6. Calcul de l'énergie de la raie manquante.

   Une méthode simple, utile mais non rigoureuse, consiste à réaliser que la valeur de la raie manquante peut se déduire approximativement de la moyenne arithmétique de la valeur des deux raies qui encadrent cette raie.

   Énergie (raie manquante) = [ E(J = 0 → J = 1) + E(J = 1 → J = 0) ] / 2

   En portant sur un graphe l'intensité de la raie en fonction de son énergie exprimée en cm^–1 (figure ci-dessous), on observe que l'on a deux groupes de raies.

   

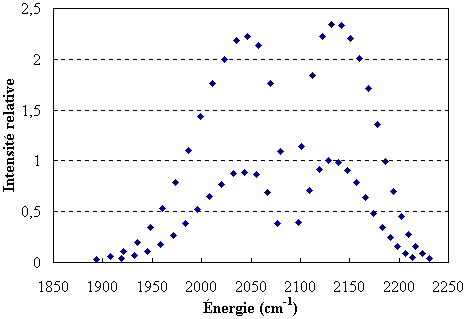
   Compte tenu des proportions isotopiques, la série de raies plus intenses correspond au D³⁵Cl et l'autre au D³⁷Cl. On peut donc constituer un tableau (voir tableau suivant) dans lequel on a regroupé dans les deux premières colonnes ce qui a trait au D³⁵Cl et dans les 5^e et 6^e colonnes ce qui correspond au D³⁷Cl. Dans le premier cas, la raie manquante aurait une énergie telle que :

   Énergie (raie manquante) = [ 2 101,62 + 2 080,27 ] / 2 = 2 090,94 cm^–1

   De la même manière, pour D³⁷Cl :

   Énergie (raie manquante) = [ 2 101,62 + 2 080,27 ] /2 = 2 090,94 cm^–1

   Énergie (raie manquante) = [ 2 098,59 + 2 077,31 ] /2 = 2 087,95 cm^–1

   Les vraies valeurs, plus rigoureuses, vont apparaître lors de la résolution de la cubique E = ¦(m), après avoir changé la variable J en m. Il est donc nécessaire d'établir pour chaque raie, sa valeur de J. Les deux séries de raies se présentent sous la forme de deux lobes, l'un plus riche en énergie que l'autre. On identifiera ainsi les raies riches et les raies pauvres dans chacun des cas. La raie la moins énergétique de la bande riche porte la valeur de J = 0 et la raie la plus énergétique de la bande pauvre porte la valeur J = 1. On peut donc remplir les colonnes 3 et 7 du tableau.

   nº	Énergie (cm–1)	JD35Cl	m	nº	Énergie (cm–1)	JD37Cl	m
   1	2230,8479	+ 15	+ 16
   2	2224,0387	+ 14	+ 15
   3	2216,9606	+ 13	+ 14	4	2213,6323	+ 13	+ 14
   5	2209,6132	+ 12	+ 13	6	2206,3007	+ 12	+ 13
   7	2202,0025	+ 11	+ 12	8	2198,7071	+ 11	+ 12
   9	2194,1272	+ 10	+ 11	10	2190,8502	+ 10	+ 11
   11	2185,9952	+ 9	+ 10	12	2182,7377	+ 9	+ 10
   13	2177,6036	+ 8	+ 9	14	2174,3672	+ 8	+ 9
   15	2168,9620	+ 7	+ 8	16	2165,7472	+ 7	+ 8
   17	2160,0666	+ 6	+ 7	18	2156,8750	+ 6	+ 7
   19	2150,9268	+ 5	+ 6	20	2147,7596	+ 5	+ 6
   21	2141,5397	+ 4	+ 5	22	2138,3978	+ 4	+5
   23	2131,9144	+ 3	+ 4	24	2128,7986	+ 3	+ 4
   25	2122,0484	+ 2	+ 3	26	2118,9605	+ 2	+ 3
   27	2111,9499	+ 1	+ 2	28	2108,8904	+ 1	+ 2
   29	2101,6186	0	+ 1	30	2098,5888	0	+ 1
   	raie manquante				raie manquante
   31	2080,2753	+ 1	- 1	32	2077,3076	+ 1	- 1
   33	2069,2694	+ 2	- 2	34	2066,3342	+ 2	- 2
   35	2058,0468	+ 3	- 3	36	2055,1451	+ 3	- 3
   37	2046,6072	+ 4	- 4	38	2043,7399	+ 4	- 4
   39	2034,9590	+ 5	- 5	40	2032,1271	+ 5	- 5
   41	2023,1001	+ 6	- 6	42	2020,3044	+ 6	- 6
   43	2011,0405	+ 7	- 7	44	2008,2814	+ 7	- 7
   45	1998,7764	+ 8	- 8	46	1996,0555	+ 8	- 8
   47	1986,3186	+ 9	- 9	48	1983,6365	+ 9	- 9
   49	1973,6637	+ 10	- 10	50	1971,0211	+ 10	- 10
   51	1960,8216	+ 11	- 11	52	1958,2191	+ 11	- 11
   53	1947,7905	+ 12	- 12	54	1945,2297	+ 12	- 12
   55	1934,5784	+ 13	- 13	56	1932,0590	+ 13	- 13
   57	1921,1853	+ 14	- 14	58	1918,7094	+ 14	- 14
   59	1907,6167	+ 15	- 15
   60	1893,8780	+ 16	- 16

   On peut essayer de porter sur un graphe les valeurs des énergies de chacune des raies en fonction de J (figure 1). On voit que ces courbes ne permettent pas d'obtenir la valeur de l'énergie de la transition vibrationnelle pure en utilisant l'ensemble des données numériques.

   
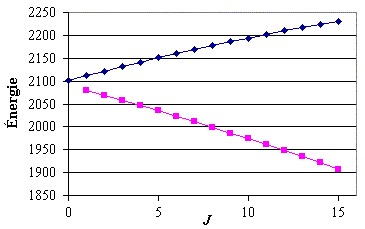
   Figure 1. Variation de l'énergie des raies en fonction de J (cas D³⁵Cl).

   Après avoir identifié les valeurs de J, il convient d'effectuer les changements de variables appropriés. Pour les raies riches, le changement de variables est tel que m = J + 1 et pour les raies pauvres, m = –J. On constitue ainsi les 4^e et 8^e colonnes du tableau précédent. Pour compléter les calculs, il ne reste plus qu'à effectuer une régression d'ordre 3 en m sur chacune des deux molécules.

   ΔE  =  b + am + cm² + dm³

   Dans cette équation :

   • l'ordonnée à l'origine b est l'énergie de la transition vibrationnelle pure, égale à ω_e – 2 ω_ex_e;
   • a  =  B″ + B′, où B″ et B′ sont les constantes rotationnelles dans chacun des deux niveaux de vibration;
   • c  =  B″ – B′;
   • d = – 4 D, où D est la constante de distorsion centrifuge.

   L'utilisation d'un chiffrier, ou encore d'un logiciel graphique ou statistique, établit les deux relations suivantes :

   Figure 2 : y (D³⁵Cl)  =   –0,0006 m³ – 0,1121 m² + 10,6719m + 2091,0506
   
   R ² = 1,0000

   
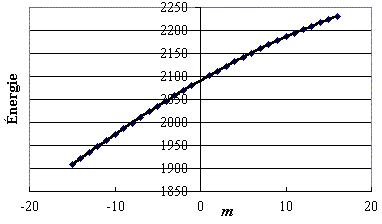
   Figure 2. Énergie des raies en fonction de m (cas D³⁵Cl).

   Figure 3 : y (D³⁷Cl)  =   –0,0006 m³– 0,1117 m² + 10,6409 m + 2088,0547
   
   R ² = 1,0000

   
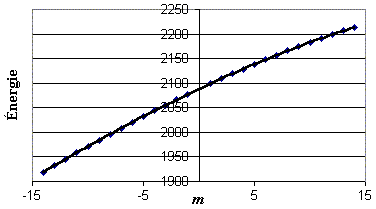
   Figure 3. Énergie des raies en fonction de m (cas D³⁷Cl).

   On obtient donc les valeurs suivantes :

   Molécule	ωe – 2 ωexe (cm–1)	B′ (cm–1)	B″ (cm–1)	D (cm–1)
   D35Cl	2091,0516	5,3918	5,2797	1,5 10–4
   D37Cl	2088,4893	5,3763	5,2646	1,5 10–4

   On notera que les valeurs de ω_e sont significativement différentes des moyennes arithmétiques calculées en début de problème.

7. Réponses :

   B′ (D³⁵Cl, υ = 0)  =  5,3922 cm^–1;    B″ (D³⁵Cl, υ = 2)  =  5,1684 cm^–1.

8. La relation qui existe entre la constante de rotation et le niveau de vibration est :

   B_υ  =  B_e – α_e (υ + 1/2) + ...

   On peut dès lors compléter le tableau qui suit et noter la bonne coïncidence entre les résultats théoriques et ceux obtenus précédemment.

   υ	B (cm–1)
   	théorique	problèmes 6 et 7
   0	5,392 215	5,392 2
   1	5,278 857	5,2797
   2	5,165 566	5,168 4

9. Si I est le moment d'inertie, μ la masse réduite et r la longueur de la liaison, alors la constante de rotation B est donnée par :

   

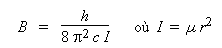
   La constante de rotation d'une molécule diatomique varie comme l'inverse de la distance internucléaire au carré. Donc sur un graphe, si l'on porte la grandeur B en fonction de l'inverse de cette distance au carré on doit obtenir une droite. C'est ce que montre le graphe qui suit. Notons que le coefficient de corrélation R ² est bien égal à l'unité.

   
   
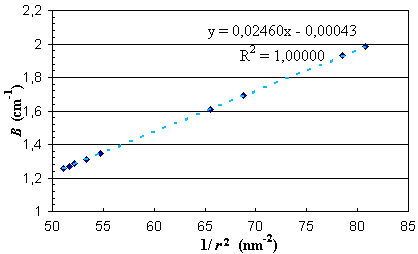
   Figure 4. Variations de B en fonction de l'inverse du carré de la longueur de la liaison C=O.

   Par ailleurs, le module n'apporte pas de réponse quant à une éventuelle dépendance de ω_e en fonction de la longueur de la liaison. Le tableau des données indiqué plus haut montre que ω_e diminue avec l'allongement de la liaison. Cela est confirmé par le graphe qui suit. Cette figure ne précise évidemment pas le type de relation entre les deux grandeurs.

   

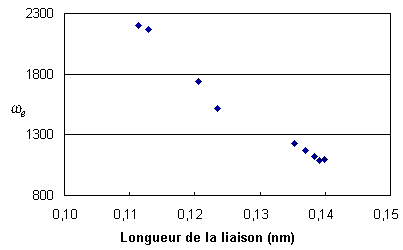
   L'obtention d'une courbe de tendance peut parfois aider à préciser cette dépendance. Une régression linéaire et une régression polynomiale d'ordre 2 donnent les équations suivantes :

   y  =  – 3854,1 x + 6 439,8 avec R ² = 0,9762

   y  =  – 8398,7 x² – 25040 x + 19 693 avec R² = 0,9945

   Le coefficient de corrélation donne un avantage à la dépendance quadratique de ω_e sur la longueur de la liaison. La différence, pour significative qu'elle soit, n'est pas suffisante pour confirmer cette dépendance.

10. Ce problème est simple à solutionner. Il s'agit seulement de traduire en chiffres la relation suivante :

    

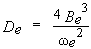
    D'où :

    

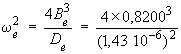
    ω_e²  =  1,542 × 10⁶ (cm^–1)²

    et ω_e = 1 240 cm^–1

    La valeur ainsi calculée est inférieure à la valeur observée qui est de 1 285,08 cm^–1, soit un écart d’environ 3,5 %.

Corrigés des problèmes avec VR Molécules

1. Les constantes apparaissent dans l'expression du terme spectral, où la constante rotationnelle B inclut la correction due à l'interaction vibration-rotation :

   E(υ, J)  =  G(υ) + F(J)
   
   E(υ, J)  =   ω_e (υ + 1/2) – ω_ex_e (υ + 1/2)² +  [ B_e – α_e (υ + 1/2) ] J (J + 1)

   Pour un maximum de précision, on emploiera les plus grandes valeurs possibles des nombres quantiques.

   Pour ω_e, on utilise l'énergie du niveau υ = 5, avec J = 0 et l'anharmonicité désactivée. On trouve :

   ω_e  =  16 450 / 5,5  = 2 990,9 cm^–1

   Pour ω_ex_e, on évalue, toujours pour le niveau υ = 5, la différence d'énergie ΔE avec et sans l'anharmonicité, égale à ω_ex_e (υ + 1/2)². On trouve :

   ω_ex_e  =  ΔE (υ, J) / (υ + 1/2)²  =  (16 450 – 14 850) / 5,5²  =  53 cm^–1.

   B_e est déterminé à partir de l'énergie pour J = 30 :

   

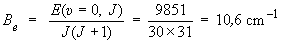
   Finalement, α_e est déterminé à partir de la différence d'énergie ΔE, pour υ = 5 et J = 30, avec et sans interaction vibration-rotation, égale à :

   α_e (υ + 1/2) J (J + 1)

   On trouve :

   

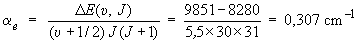
2. Les masses réduites de H₂ et HD sont respectivement égales à 1/2 et 2/3. Le rapport μ / μ_i est donc égal à 3/4.

   Le rapport B_e,i / B_e est égal à 42 500 / 56 540  =  0,752, ce qui est conforme à l'équation 3.7.

   Le rapport ω_e,i / ω_e est égal à 20 970 / 24 170  =  0,868, une valeur proche de la racine carrée de μ / μ_i (0,866), prédite par l'équation 3.8.

   Le rapport ω_e,ix_e,i / ω_ex_e est égal à (20 970 – 18 190) / (24 170 – 20 500)  =  0,757, ce qui est conforme à l'équation 3.9.

3. Employez la même méthode qu'au problème VR Molécules nº 1, et vérifiez vos réponses dans le WebBook du site du NIST : http://webbook.nist.gov/chemistry/name-ser.html. Note : Les constantes correspondant à la molécule dans son état électronique fondamental sont à la dernière ligne des tableaux.