|
|
MODULE 4 Diffusion de
la lumière - effet Raman
Problèmes
Les intervalles entre les niveaux d'énergie de
vibration de H2, HD et D2 peuvent
être estimés à partir des spectres de
diffusion Raman. Ils mesurent respectivement
4 401,2, 3 813,1 et 3 115,5 cm–1.
Calculez la constante de force dans les systèmes
C.G.S. et SI du ressort physique équivalent pour
les trois espèces isotopiques mentionnées
de l'hydrogène. Corrigé
-
Lorsque l'acétylène est
irradié à 435,83 nm, une raie Raman
attribuée à l'élongation
longitudinale symétrique est observée
à 476,85 nm. Calculez la fréquence
fondamentale en Hz et l'énergie en cm–1
de cette vibration. Corrigé
-
Lorsque HCl est irradié avec la
raie du mercure à 253,65 nm, indiquez en nm
où l'on doit retrouver la raie Stokes
correspondant à la transition vibrationnelle pure,
υ = 0 → υ = 1.
On donne pour HCl : ωe = 2 990,9 cm–1
et ωexe = 52,8 cm–1
Corrigé.
Corrigés
-
Le module 2,
qui traite de la vibration, établit la constante
de force, k, de l'oscillateur harmonique de la
manière suivante :
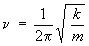
On se rappelle aussi que  = ν / c.
En remplaçant m, la masse de l'oscillateur,
par la masse réduite μ, on
obtient :
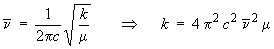
4 π2
c2 = 4 × π2
× (2,9979 × 1010)2
cm2
s–2 = 354,81 × 1020
cm2 s–2
On obtient les résultats
suivants :
|
|
(cm–1)
|
2
(cm–2)
|
m1 (g/mol)
|
m2 (g/mol)
|
<μ (g/mol)
|
k (dynes/cm)
|
k (N/m)
|
|
H2
|
4401,2
|
1,937 × 107
|
1
|
1
|
1/2
|
57,08 × 104
|
570,8
|
|
HD
|
3813,1
|
1,454 × 107
|
1
|
2
|
2/3
|
57,13 × 104
|
57,13
|
|
D2
|
3115,5
|
0,971 × 107
|
2
|
2
|
1
|
57,21 × 104
|
572,1
|
Exemple de calculs pour H2
(dans le système C.G.S.) :
k = 4 π2c2
2μ
k = 354,81 × 1020
× 1,937 × 107 × (1/2
×
1 / 6,022 × 1023)
k = 57,08 × 104
dynes/cm
Pour transformer une force exprimée
dans le système C.G.S. en newtons (système
SI), il faut se souvenir que
F = mg (ou μg) et que
son équation aux dimensions est MLT
–2. Pour obtenir la même valeur
en SI, calculons le rapport suivant :
⇒
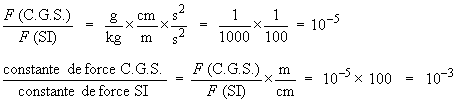
57,12 × 104 dynes/cm
=
(57,12 × 104) × 10–3
= 571,2 N/m
k = 571,2 N/m
-
La longueur d'onde incidente est λinc. = 435,83 nm
et la longueur d'onde diffusée est λdiff.=
476,85 nm. L'énergie incidente et
l'énergie diffusée sont calculables :
Einc. (cm–1) = 1 / (435,83 × 10–7)
et
Ediff. (cm–1) = 1 / (476,85 × 10–7)
L'énergie manquante a
été prise par la molécule pour
augmenter son énergie vibrationnelle (transition
υ = 0 → υ = 1) :
E = (1/435,83
– 1/476,85) × 107
cm–1 = 1 974 cm–1
La fréquence de la transition
(observée en infrarouge) est donnée par la
relation :
c = ν = (2,998 × 1010 cm/s) × 1 974
cm–1
ν = 5,913 × 1013
Hz ou s–1
-
L'énergie du niveau de vibration
υ, exprimée en nombre d'ondes,
s'écrit :
= E /
hc = G(υ)
= ωe (υ
+ 1/2) – ωexe
(υ + 1/2)2
Pour le passage de υ = 0
à υ = 1, on a :
transition
= G(1) –
G(0) = ωe
– 2 ωexe = 2990,9
– 2 × 52,8
= 2 885,3 cm–1
L'énergie en cm–1
et la longueur d'onde sont reliées par :
= ν / c
et λ = c / ν ⇒
ν = c / λ
⇒ = 1 / λ
La longueur d'onde de la raie Raman peut
ainsi être déterminée à partir
des énergies associées à la
radiation incidente et à la transition :
λinc. = 253,65
nm = 253,65 × 10–7
cm
inc. =
× 107 / 263,65
=
3,9424 × 104 cm–1 = 39
424 cm–1
Raman
= inc. – transition
= 39 424 – 2
885 = 36 539 cm–1
λ
Raman = 1 / Raman =
1 / 36 539 = 2,7368 × 10–5
cm
λRaman =
273,68 nm
|
