MODULE 6  Rotation des molécules polyatomiques

Problèmes

1. La molécule 0=C=S est linéaire et les longueurs 0=C et C=S sont respectivement égales à 0,116 et 0,156 nm. Situez la position du centre de masse de la molécule, et calculez son moment d'inertie dans le système SI.

   Mêmes questions pour la molécule N=N=O; les longueurs des liaisons N=N et N=O sont respectivement égales à 0,115 et 0,123 nm. Corrigé

2. Une série de raies rotationnelles de la molécule d'hydrogène est observée en spectroscopie électronique dans la région de l'ultraviolet sous vide (υ' ← υ : 3' ← 0) :

   E (cm–1)
   94 058,57	93 410,17	92 010,92
   94 003,30	93 315,81	91 845,79
   93 908,26	93 030,70	91 370,61
   93 861,08	92 912,75	91 181,89
   93 702,69	92 564,29	90 643,35
   93 631,92	92 422,74	89 829,15

   Calculez B' et B, r_e' et r_e, ainsi que la position de la raie ₀₃. Pour ce faire, indexez convenablement les raies (J et m) et tracez la parabole de Fortrat, en utilisant un moyen électronique approprié pour calculer les coefficients du polynôme E  =  d + am + cm² Corrigé.

3. Faites de même pour la série correspondant à la transition (4' ← 0) :

   E (cm–1)
   95 253,64	94 600,47	93 172,58
   95 193,60	94 477,47	92 957,34
   95 105,72	94 213,84	92 517,96
   95 044,22	94 060,10	92 271,96
   94 897,76	94 737,88	91 773,99
   94 805,51	94 553,38

4. Les raies, exprimées en nombre d'onde, E (cm^–1), mesurées dans le spectre électronique d'un hydrure diatomique sont indiquées dans le tableau qui suit. Déterminez pour chaque raie, les valeurs de J en utilisant la méthode des différences.

   30 005,03	30 094,82	30 127,92	30 148,97	30 203,40
   30 024,67	30 110,25	30 133,81	30 150,65	30 211,25
   30 043,47	30 113,61	30 138,87	30 174,78	30 218,26
   30 061,43	30 121,18	30 143,08	30 185,16	30 224,43
   30 078,55	30 124,84	30 146,44	30 194,70	30 229,76

   Tracez la parabole de Fortrat et, sur le même graphe, identifiez les branches P, Q et R. Calculez également les valeurs de B et de B' dans les états électroniques concernés. Corrigé

5. En spectroscopie électronique, une bande d'absorption du ³⁵Cl₂ sous très haute résolution montre une série de raies données dans le tableau suivant. En utilisant la méthode de la deuxième différence, établissez les valeurs de J, m, les branches P et R. Tracez la parabole de Fortrat.

   18 147,85	18 146,91	18 145,02	18 141,87
   18 147,81	18 146,66	18 144,41	18 140,34
   18 147,71	18 146,25	18 143,94	18 138,64
   18 147,60	18 145,93	18 143,23	18 136,76
   18 147,22	18 145,42	18 142,69	18 134,71

   Calculez les valeurs de B et de B' dans les états électroniques concernés, ainsi que les distances internucléaires correspondantes.

6. Démontrez les expressions données dans le module pour les moments d'inertie de la molécule BrF₅. Corrigé

Problèmes avec VR Molécules

1. Placez VR Molécules à la page 5. En mesurant les distances internucléaires à l'aide de la grille, déterminez la valeur du moment d'inertie de la molécule HCN. À partir de cette valeur, calculez la constante de rotation B et comparez-la avec la valeur qui peut être déduite de l'énergie de rotation affichée par VR Molécules pour J = 10. Corrigé

2. Placez VR Molécules à la page 6. En mesurant les distances internucléaires à l'aide de la grille, déterminez la valeur du moment d'inertie de la molécule C₂H₂. À partir de cette valeur, calculez la constante de rotation B et comparez-la avec la valeur qui peut être déduite de l'énergie de rotation affichée par VR Molécules pour J = 10. Corrigé

3. Placez VR Molécules à la page 7. En mesurant, à l'aide de la grille, les longueurs appropriées, déterminez la valeur des moment d'inertie I_par et I_perp de la molécule SO₃. À partir de la valeur de I_perp, calculez la constante de rotation B et comparez-la avec la valeur qui peut être déduite de l'énergie de rotation affichée par VR Molécules pour J = 10. Corrigé

Corrigés

1. La distance de l'atome de soufre au centre de masse est calculée à l'aide de la relation suivante :

   

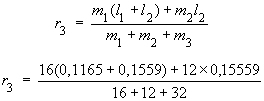
   r₃  =  0,1038 nm

   Remarque : Point n'est besoin de diviser les masses par le nombre d'Avogadro puisque ce même facteur se retrouve au numérateur et au dénominateur.

   Dans le cas de N=N=O, on montre, de la même façon, que le centre de masse est pratiquement confondu avec l'atome d'azote central.

   De leur côté, les moments d'inertie sont donnés par la relation :

   

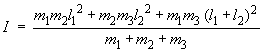
   Il ne reste qu'à remplacer chaque valeur littérale par sa valeur numérique. Pour O=C=S, on obtient :

   

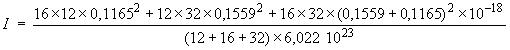
   I = 0,1382 10^–41 = 1,382 10^–42 m² g

   I = 1,382 10^–45 kg m²

   On procède de la même manière pour N=N=O. On obtient :

   I = 7,05 10^–46 kg m²

2. La difficulté première de ce problème réside dans la détermination des raies appartenant respectivement à la bande pauvre et à la bande riche. Pour « démêler » les deux groupes de raies on peut utiliser deux techniques de manière complémentaire : la première est visuelle; la seconde, arithmétique, est appelée la méthode de la deuxième différence.

   La première méthode consiste à porter sur un axe horizontal gradué en cm^–1 la position de chacune des raies, position représentée par un trait vertical de 1 à 2 cm de longueur (voir figure ci-dessous). Une fois ce travail de dessin terminé, on cherchera à regrouper les raies dans deux suites de raies, chacune révélant une progression constante dans l'espacement inter-raie.

   
   
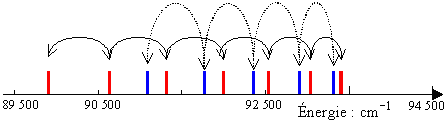
   Positionnement des raies et agencement des deux groupes (riche et pauvre).

   On se rend ainsi visuellement compte que les raies ainsi constituées :

   89 829,15 – 90 643,35 – 91 370,61 – 92 010,92 …

   forment une suite dont l'interespace diminue régulièrement.

   Il est alors temps d'utiliser la deuxième différence pour constituer de manière plus rigoureuse les deux groupes de raies. La première différence entre les deux raies tout juste indiquées est telle que :

   ΔE  =  90 643,35 – 89 829,15  =  814,20 cm^–1.

   La différence entre les deux raies suivantes donne :

   ΔE  =  89 829,15 – 91 370,61  =  727,26 cm^–1.

   La deuxième différence :

   Δ[ΔE]  =  814,20 – 727,26  =  86,94 cm^–1

   Une propriété des courbes quadratiques (paraboliques) réside dans le fait que la deuxième différence doit être constante. On choisira donc les raies de telle manière que cette propriété soit respectée dans chacune des deux branches (riche et pauvre). On peut dès lors, de proche en proche, construire le tableau qui suit. On porte dans la colonne médiane, les valeurs en cm^–1 des raies observées. Puis, de part et d'autre de cette colonne on calcule la première différence de chacune des branches. Enfin, dans les deux colonnes extrêmes, on indique les deuxièmes différences.

   Notez qu'à moins d'avoir fait d'abord l'analyse graphique on doit procéder par essais et erreurs pour déterminer s'il faut calculer les premières différences entre deux raies successives ou à toutes les deux raies, selon que l'on se trouve en dehors ou dans la zone commune des deux branches, zone que l'on ne connaît pas a priori.

   Δ[Δ[E(cm–1)]]	Δ[E(cm–1)]	E(cm–1)	Δ[E(cm–1)]	Δ[Δ[E(cm–1)]]
   		94 058,57
   	55,27
   86,95		94 003,30
   	142,22	93 908,26
   86,94		93 861,08	205,57
   	229,16	93 702,69		86,95
   86,95		93 631,92	292,52
   	316,11	93 410,17		86,95
   86,95		93 315,81	379,47
   	403,06	93 030,70		86,94
   86,95		92 912,75	466,41
   	490,01	92 564,29		86,96
   86,94		92 422,74	553,37
   	576,95	92 010,92		86,94
   86,95		91 845,79	640,31
   	663,90	91 370,61		86,95
   		91 181,89	727,26
   		90 643,35		86,94
   			814,20
   		89 829,15
   Bande riche R			Bande pauvre P

   L'étape suivante consiste à identifier laquelle des deux branches constitue la bande riche et laquelle la bande pauvre. Dans un tel ensemble de raies, la bande qui contient la raie la plus énergétique, ici la raie située à 94 058,57 cm^–1, est la bande riche. Il reste à identifier pour chacune des raies quelle est sa valeur J (le nombre quantique de rotation), puis à effectuer le changement de variable J → m selon les conditions déjà vues : m = –J pour les raies pauvres et m = J + 1 pour les raies riches (voir tableau et graphes qui suivent).

   Réponse du calculateur :

   E(cm^–1)  =  94 026,9 + 75,1523 m – 43,4737 m²  =  d + am + cm²

   Pour terminer le problème, il reste à donner la signification physique de chacun des facteurs de l'équation en m². L'ordonnée à l'origine, d, représente la transition électronique pure, soit :

   ₀₃  =  94 026,9 cm^–1

   Les valeurs de la constante rotationnelle dans l'état électronique fondamental et dans l'état électronique excité, B et B', sont telles que B + B' = a et B – B' = c.

   On obtient :

   B  =  59,313 cm^–1     et     B'  =  15,839 cm^–1

   Ces valeurs permettent de calculer la longueur de la liaison dans chacun des deux états électroniques :

   r_e =  0,0751 nm     et     r_e'  =  0,1453 nm

   On le voit bien ici, les deux états électroniques sont géométriquement très différents : la liaison a presque doublé de longueur. Cela entraîne une modification importante des constantes B et B' de telle sorte que la courbe monotone croissante que l'on observait en spectroscopie vibrationnelle est toujours une parabole mais n'est plus monotone croissante; elle atteint un maximum pour une valeur de m donnée, pour diminuer par la suite.

4. Une première méthode basée sur l'essai et erreur vise à rechercher et regrouper les raies de telle manière que la seconde différence demeure constante (tableau suivant). Cette méthode n'est pas toujours facile d'usage. Notons que dans le cas présent le regroupement est facilité par le fait que les huit raies les plus énergétiques ont une seconde différence approximativement constante : Δ(ΔE) = 0,84 cm^–1; elles appartiennent à la branche R. Il en est de même des sept raies les moins énergétiques, que l'on peut associer à la branche P. Les raies médianes se regroupent dans une troisième branche Q après avoir exclu une raie qui s'incorpore à la branche P.

   m	J	E(cm–1)	Δ[E(cm–1)]	Δ[Δ[E(cm–1)]]	Commentaires
   –9	9	30 005,03			Branche P
   			19,64
   –8	8	30 024,67		0,84
   			18,80
   –7	7	30 043,47		0,84
   			17,96
   –6	6	30 061,43		0,84
   			17,12
   –5	5	30 078,55		0,85
   			16,27
   –4	4	30 094,82		0,84
   			15,43
   –3	3	30 110,25		0,84
   			14,59
   –2	2	30 124,84
   	2	30 113,61			Branche Q
   			7,57
   3	3	30 121,18		0,83
   			6,74
   4	4	30 127,92		0,85
   			5,89
   5	5	30 133,81		0,83
   			5,06
   6	6	30 138,87		0,85
   			4,21
   7	7	30 143,08		0,85
   			3,36
   8	8	30 146,44		0,83
   			2,53
   9	9	30 148,97		0,85
   			1,68
   10	10	30 150,65
   3	2	30 174,78			Branche R
   			10,38
   4	3	30 185,16		0,84
   			9,54
   5	4	30 194,70		0,84
   			8,70
   6	5	30 203,40		0,85
   			7,85
   7	6	30 211,25		0,84
   			7,01
   8	7	30 218,26		0,84
   			6,17
   9	8	30 224,43		0,84
   			5,33
   10	9	30 229,76

   L'agencement des raies à l'intérieur de chacune des branches P, Q et R peut se faire d'une manière simple en portant sur un même axe gradué en cm^–1 les raies observées. La raie la plus énergétique appartient à la bande riche, la branche R, et celle la moins énergétique à la bande pauvre, la branche P. Les autres sont à regrouper à l'intérieur de la branche Q ou de l'une ou l'autre des branches P et R. Un simple examen visuel, à qui est un peu habitué, permet de reconnaître une suite, une progression constante et régulière, des différences d'énergie des 8 raies les plus énergétiques. On en calcule les différences et les secondes différences. Cela permet de conforter les résultats obtenus avec le tableau précédent.

   Une fois les raies convenablement regroupées dans chacune des branches P, Q et R, il faut leur attribuer la valeur de J. Le premier essai est de partir avec la valeur J = 0. Ainsi les premières raies des branches Q et R auront la valeur J = 0 et la première raie de la branche pauvre sera indicée J = 1 (transition J = 1 → J = 0). Un graphe de l'énergie des raies en fonction de m produit une courbe discontinue à m = 0. On doit soupçonner une erreur dans l'attribution des valeurs J à chacune des raies.

   
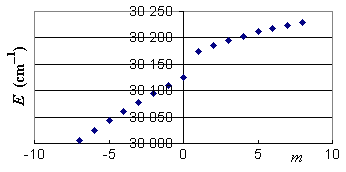
   La valeur de J_min est 0

   On peut soupçonner que la molécule est de type toupie symétrique. Dans ce cas, les premières valeurs de J ne sont pas disponibles. On essaie donc la même opération en notant la première raie avec la valeur J = 1.

   Si le niveau J = 1 est disponible, on doit observer les transitions suivantes :

   • branche R : J = 1 vers J' = 2; avec le changement de variable m = J + 1, m passe de m = 2 à m' = 3;

   • branche Q : J = 1 vers J' = 1; avec le changement de variable m = J, m passe de m = 1 à m' = 1;

   • branche P : J = 2 vers J' = 1; avec le changement de variable m = –J, m passe de m = –2 à m' = –1.

   Les trois segments de courbes ont les équations analytiques suivantes :

   • branche R : y  =  – 0,421 19 x² + 12,48714 x + 30151,49048; R² = 1,000 00;

   • branche P : y  =  – 0,421 19 x² + 12,482 86 x + 30151,490 48; R² = 1,000 00;

   • branche Q : y  =  – 0,421 08 x² - 0,419 84 x + 30151,49238; R² = 1,000 00.

   

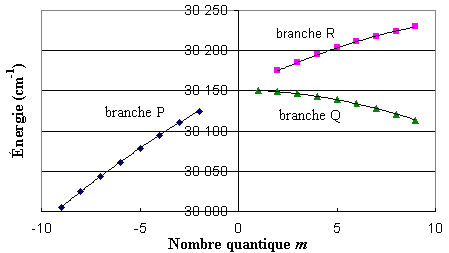
   Cette fois la concordance est bien meilleure. Les expressions analytiques des branches P et Q sont pratiquement semblables. En outre, l'interception des trois courbes avec l'axe des ordonnées est identique, à 30 151,49 cm^–1. Cette dernière valeur correspond à la transition électronique pure. Une seule courbe intégrant les données des branches P et R a l'expression analytique suivante :

   • branches P et R : y  =  – 0,421 00 x² + 12,485 00 x + 30151,49 ; R² = 1,000 00

   

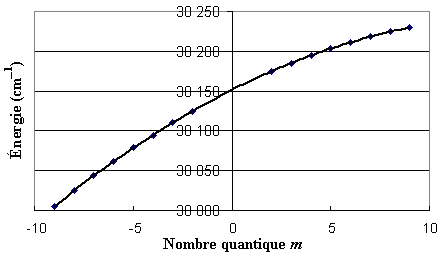
   En se rappelant que la somme B + B' est identique au coefficient de x et que la différence B – B' est identique au coefficient de x², on obtient :

   B + B'  =  12,485 cm^–1    et    B' –B  =  – 0,421 cm^–1

   D'où :

   B'  =  6,032 cm^–1    et    B  =  6,453 cm^–1

   La constante B diminue de manière significative (environ 7 %) en passant de l'état fondamental vers l'état électronique excité. On a donc une modification importante de la distance internucléaire moyenne, qui augmente d'environ 3,5 %.

6. La molécule BrF₅ est constituée d'un carré dont chacun des sommets est occupé par un atome de fluor, et le centre par l'atome de brome. Le cinquième atome de fluor est situé sur l'axe de symétrie d'ordre 4, en dehors de ce plan carré (voir figure ci-dessous). Soient r₁ les longueurs des liaisons BrF dans le plan carré et r₂ celle de BrF en dehors du plan carré. Le centre de masse, G, est nécessairement situé sur l'axe de symétrie. Soit a la distance entre l'atome de brome et G. On a donc :

   a + b  =  r₂     ou encore     b  =  r₂ – a

   

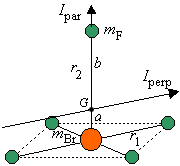
   Par ailleurs, la position du centre de masse est définie par la relation :

   m_F b  =  m_Br a + 4 m_F a

   En remplaçant b par la valeur obtenue plus tôt, on obtient :

   m_F (r₂ – a)  =  m_Br a + 4 m_F a

   ce qui se réécrit :

   m_F r₂ – m_F a  =  m_Br a + 4 m_F a

   m_F r₂  =  m_Br a + 4 m_F a + m_F a  =  Σm_i a

   Σm_i est la somme des masses des atomes constitutifs de la molécule. Finalement, en réarrangeant cette dernière expression, on obtient :

   a  =  m_F r₂ / Σm_i

   La position du centre de masse est donc complètement définie en termes de la distance et des masses des atomes constituant la molécule.

   Calculs des moments d'inertie de BrF₅

   Le moment d'inertie parallèle à l'axe de symétrie, noté I_par, n'est dû qu'aux quatre atomes de fluor du carré; il est simplement donné par la relation suivante :

   I_par  =  4  m_F r₂²

   Le moment d'inertie perpendiculaire à l'axe de symétrie, noté I_perp, est donné par la relation suivante :

   I_perp  =   m_Br a² + m_F b² + 2 m_F a² + 2 m_F (r₁² + a²)

   I_perp  =   m_Br a² + m_F b² + 2 m_F a² + 2 m_F r₁² + 2 m_F a²

   I_perp  =   m_Br a² + m_F (r₂ – a)² + 2 m_F a² + 2 m_F r₁² + 2 m_F a²

   I_perp  =   m_Br a² + m_F (r₂²– 2ar₂ + a²) + 2 m_F a² + 2 m_F r₁² + 2 m_F a²

   I_perp  =   m_Br a² + m_F r₂² – 2 m_F ar₂ + m_F a² + 2 m_F a² + 2 m_F r₁² + 2 m_F a²

   I_perp  =    a² Σm_i + 2 m_F r₁² + m_F r₂² – 2 am_F r₂

   Il ne reste plus maintenant qu'à remplacer a par la valeur établie plus haut :

   

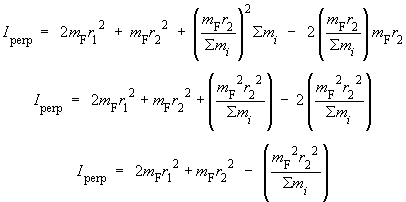
   On obtient bien l'équation donnée dans le module :

   

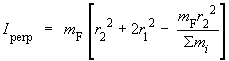
   La valeur du moment d'inertie perpendiculaire à l'axe de symétrie est donc, elle aussi, entièrement déterminée par les données relatives à la structure et à la composition de la molécule.

Corrigés des problèmes avec VR Molécules

1. Les distances au centre de masse des atomes N, C et H sont respectivement 61 pm, 56 pm et 163 pm.

   Le moment d'inertie est donc donné par :

   

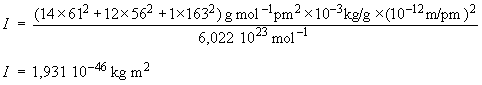
   et la constante B est donnée par :

   

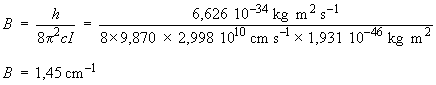
   ce qui est proche de la valeur qu'on peut déduire à partir des informations fournies dans VR Molécules. En effet, B est égal à la moitié de l'énergie à J = 1, soit 1,48 cm^–1.

 

2. Les distances au centre de masse des atomes C et H sont respectivement 60 pm et 168 pm. De la même façon qu'à l'exercice précédent, on trouve :

   I  =  2 (12 × 60² + 1 × 168² ) / 6,022 × 10⁵⁰  =  2,372 × 10^–46 kg m²

   d'où B  =  1,18 cm^–1, ce qui est égal à la valeur obtenue dans VR Molécules.

3. Le distance au centre de masse des atomes d'oxygène est de 142 pm. Le moment d'inertie I_par est simplement égal à trois fois le moment d'inertie d'un atome d'oxygène par rapport à l'axe de symétrie de la molécule, soit, en SI :

   I_par  =  3 × 16 g mol^–1  × 10^–3 kg/g × (142 × 10^–12 m)² / 6,022 × 10²³ mol^–1  =  1,607 × 10^–45 kg m²

   De son côté, le moment I_perp est égal à deux fois le moment d'inertie d'une molécule d'oxygène par rapport à un axe passant par une des liaisons S-O (pointillés dans la figure ci-dessous). On trouve  :

   

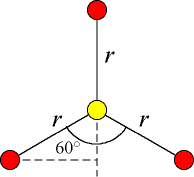
   I_perp  =  2 × 16 × 10^–3 × (142 × 10^–12 × sin 60°)² / 6,022 × 10²³  =  0,803 × 10^–45 kg m²

   d'où l'on tire, de la même manière que précédemment, B  =  0,35 cm^–1, ce qui est à peu près égal à la valeur obtenue dans VR Molécules.