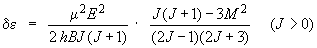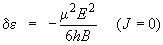|
|
MODULE 6 Rotation des
molécules polyatomiques
Préambule
La molécule diatomique tourne sur
elle-même. Qu'en est-il d'une molécule
polyatomique? Est-ce que les lois, la quantification des
niveaux d'énergie, les règles de
sélection sont conservées? L'utilisation de la
mécanique quantique est-elle toujours aussi
féconde dans la détermination de la structure
moléculaire? Que se passe-t-il si l'on applique un
champ électrique important aux molécules en
même temps que l'excitation infrarouge?
Molécules polyatomiques
linéaires

Le modèle mécanique choisi pour
représenter la molécule diatomique (voir
module 1) peut
s'étendre aux molécules polyatomiques
linéaires. La mécanique quantique permet de la
même façon d'obtenir les niveaux
d'énergie de rotation possibles. La formule est
identique à celle correspondant aux molécules
diatomiques :
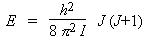
soit le terme spectral :
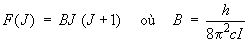
I est le moment d'inertie de la
molécule (il est unique).
Les niveaux d'énergie ont la
même disposition que dans les molécules
diatomiques. Cependant, avec l'augmentation du nombre
d'atomes et l'accroissement de la longueur des
molécules, le moment d'inertie s'accroît, ce
qui se traduit par une diminution de la constante de
rotation B (tableau 6.1). Les niveaux sont donc
de plus en plus rapprochés; les transitions
correspondent à des quanta
dont les fréquences sont de plus en plus loin dans le
domaine des hyperfréquences. C'est dans la
région correspondant à des longueurs d'onde de
1 mm à 10 cm (fréquences de
3 × 105 MHz à
3 × 103 MHz) que la plupart
des études sur les molécules polyatomiques
linéaires ont été
effectuées.
Tableau 6.1. Quelques
valeurs de la constante de rotation de molécules
linéaires.
|
Molécule
|
B(cm–1)
|
Molécule
|
B(cm–1)
|
|
H–12Cº14N
|
1,478 705
|
35Cl–12Cº14N
|
0,199 231
|
|
16O=12C=32S
|
0,202 923
|
H–12Cº12C–35Cl
|
0,189 666 8
|
|
Il faut
noter la précision donnée sur les
valeurs de B.
|
La nécessaire variation du moment
dipolaire permanent lors d'une transition se traduit par une
règle de sélection qui est encore ΔJ = ±1,
ainsi que par le fait que, tout comme les molécules
diatomiques homonucléaires, les molécules
symétriques comme le bioxyde de carbone
(CO2) ou l'acétylène
(C2H2) ne présentent pas de
spectre de rotation pure.
Un problème différent se pose
cependant. Alors que pour une molécule diatomique il
est possible de déterminer la distance
internucléaire à partir du moment
d'inertie, ici nous obtenons un seul moment d'inertie et
nous avons au moins deux distances internucléaires
à déterminer (en fait, n – 1
pour un molécule comptant n atomes).
On peut résoudre ce problème en
considérant les molécules isotopiques. La
substitution isotopique permet d'obtenir autant de moments
d'inertie qu'il y a de molécules isotopiques
disponibles.
Prenons par exemple la molécule O=C=S.
On observe les spectres de rotation pure de
16O=12C=32S et de
16O=12C=34S. On en
déduit B dans chaque cas, d'où I
qui, d'après le modèle mécanique, est
relié aux deux distances internucléaires, que
l'on peut ainsi déterminer. On peut vérifier
ensuite en effectuant le même calcul avec un autre
couple, par exemple
18O=12C=32S,
16O=13C=32S,
16O=13C=34S, etc., que les
distances internucléaires varient peu ou pas avec la
composition isotopique (voir le tableau 6.2).
Tableau 6.2. Effet de
la substitution isotopique
sur les paramètres géométriques de O=C=S.
|
Paires de
molécules
|
Distances internucléaires
(nm)
|
|
masses de O, C et S
|
C=O
|
C=S
|
|
16 12 32
16 12 32
16 12 34
16 12 32
|
16 12 34
16 13 32
16 13 34
18 12 32
|
0,1165
0,1163
0,1163
0,1155
|
0,1558
0,1559
0,1559
0,1565
|
|
Inspiré
de Moore, W. J. Physical Chemistry,
Prentice-Hall,
Englewood Cliffs, New Jersey, 1972.
|
Ce résultat n'est pas étonnant
puisque la liaison est déterminée
essentiellement par le nuage électronique qui ne
change pas au cours de la substitution isotopique. Le
tableau doit se lire ligne par ligne : les constantes
B sont obtenues pour deux molécules
isotopiques (colonnes 1 et 2). Cela permet d'obtenir les
longueurs de liaisons apparaissant sur la même ligne
(colonnes 3 et 4).
Illustrons ce procédé au moyen
de l'exemple d'une molécule triatomique
linéaire (figure 6.1). Comme il n'y a que deux
liaisons dont il faut déterminer la longueur, deux
molécules isotopiquement différentes suffiront
pour obtenir les deux équations nécessaires
à la connaissance complète de la
géométrie moléculaire.
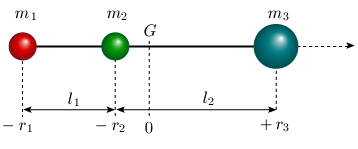
Figure 6.1. Molécule triatomique linéaire.
Les distances internucléaires (les
inconnues) sont l1 et
l2.
On désire obtenir une expression
reliant ces deux inconnues au moment d'inertie. Celui-ci est
donné par :
I =
Σi
mi ri2
= m1r12
+ m2r22 +
m3r32
D'après la figure, on a :
r1 = l1 + l2 – r3 et r2 = l2 – r3
On sait, en outre, que la position du centre
de masse G est déterminée par le fait
que la somme des moments par rapport à ce point doit
être nulle : Σi mi
ri = 0. Plaçons la
molécule sur un axe tel que l'origine de cet axe
coïncide avec le centre de masse G, ce qui
permet d'écrire :
Σi
mi ri = – m1r1
– m2r2 +
m3
r3 = 0
On substitue dans cette équation les
expressions de r1 et r2
établies plus haut :
– m1(l1 + l2 – r3)
– m2(l2 – r3)
+
m3r3 = 0
– m1(l1 + l2) – m2l2 +
m1r3 +
m2r3 +
m3r3 = 0
pour obtenir finalement :
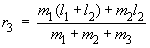
En portant cette expression et celles de
r1 et r2 établies
plus haut dans l'expression du moment d'inertie, on obtient,
après quelques manipulations algébriques,
l'équation reliant le moment d'inertie aux distances
internucléaires :
|
(6.1)
|
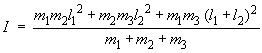
|
|
Rappelons que ces calculs ne sont valables
que pour une molécule linéaire. Or, on ne peut
déterminer à l'avance si la molécule
est linéaire ou non. Il faut donc faire cette
hypothèse a priori. Les résultats des
calculs de longueurs de liaisons fondés sur cette
hypothèse montreront sa validité.
Le tableau 6.3 présente les
valeurs obtenues à l'aide de cette technique pour
quelques molécules linéaires comptant trois
atomes ou plus.
Tableau 6.3.
Paramètres géométriques de quelques
molécules linéaires.
|
Molécules
|
Liaisons
simples
|
re
(nm)
|
Liaisons
multiples
|
re
(nm)
|
|
O=C=O
|
|
|
C=O
|
0,1162 (a)
|
|
H–CºN
|
C–H
|
0,1064
|
CºN
|
0,1156
|
|
H–N=O
|
N–H
|
0,1126
|
N=O
|
0,1191
|
|
Cl–C–N
|
C–Cl
|
0,1629
|
C–N
|
0,1163
|
|
Br–CºN
|
C–Br
|
0,1790
|
CºN
|
0,1159
|
|
H–CºC–Cl
|
C–H
|
0,1052
|
CºC
|
0,1211
|
|
C–Cl
|
0,1632
|
|
|
|
H–CºC–CºN
|
C–H
|
0,1057
|
CºN
|
0,1157
|
|
C–C
|
0,1382
|
CºC
|
0,1203
|
|
a. Valeur
obtenue à partir d'un spectre de
rotation-vibration (voir plus loin).
|
Moments d'inertie des molécules
non linéaires (ou spatiales)
Le moment d'inertie d'une molécule
rigide par rapport à un axe est donné par la
relation :
I = Σi
mi ri2
où mi est la masse
de la particule i, elle-même située
à la distance ri de cet axe.
Une molécule non linéaire (ou
spatiale) possède trois moments d'inertie
évalués selon trois axes perpendiculaires
appelés axes principaux. Dans le
système de coordonnées cartésien, ces
moments sont définis de la manière
suivante :
- Relativement à l'axe principal Oz (par
convention, l'axe de symétrie de la
molécule) le moment d'inertie de la
molécule est :
IA
= Σi
mi [(xi – x0)2
+ (yi –
y0)2]
- Relativement à l'axe principal Oy, le
moment d'inertie de la molécule est :
IB
= Σi
mi [(xi – x0)2
+ (zi –
z0)2]
- Relativement à l'axe principal Ox, le
moment d'inertie de la molécule est :
IC
= Σi
mi [(yi – y0)2
+ (zi –
z0)2]
où i représente chacun
des atomes constituant la molécule,
xi, yi et
zi les coordonnées de l'atome
i et x0, y0 et
z0 les coordonnées du centre de
masse.
Les molécules se divisent en trois
catégories selon que leurs moments d'inertie
possèdent une seule, deux ou trois valeurs
différentes.
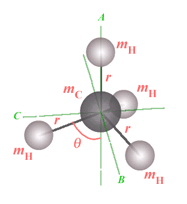
- Molécules de type sphérique

Les molécules dont les trois
moments d'inertie sont égaux sont dites de type
sphérique. Les molécules de
méthane (CH4) et de soufre
hexafluoré (SF6) font partie de cette
catégorie. Dans ces molécules, l'atome
unique (carbone ou soufre) se trouve au centre de masse
et les autres atomes (hydrogène ou fluor) sont
à une distance r du centre de masse
(figure 6.2). Dans ces conditions, on peut montrer
que l'application des formules générales
précédemment rapportées conduit
à trois moments d'inertie égaux.
|
|
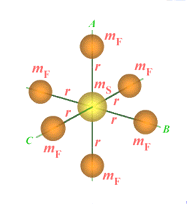
|
|
A : CH4
|
B : SF6
|
Figure 6.2.
Molécules de type sphérique.
Pour CH4 (figure 6.2A), le
calcul du moment d'inertie par rapport à un axe
contenant une liaison C–H ne fait pas intervenir
cette liaison. Les trois autres atomes d'hydrogène
sont donc seuls à contribuer au moment d'inertie.
On montre de cette manière que :
I = 8/3 mH r2
r est la longueur de la liaison C–H.
De son côté, la
molécule SF6 (figure 6.2B) est
constituée d'un carré d'atomes de fluor au
centre duquel se trouve l'atome de soufre; les deux
autres atomes sont situés sur l'axe
perpendiculaire à ce carré, à la
même distance de l'atome de soufre que les autres
atomes. On voit aisément que le moment d'inertie
est donné par la relation :
I
= 4 mF r2
- Molécules de type toupie symétrique

Les molécules avec deux moments
d'inertie égaux sont dites de type toupie
symétrique. Cette catégorie de
molécules comprend, entre autres, l'ammoniac
(NH3), le chlorure de méthyle
(CH3Cl) et le pentachlorure de phosphore
(PCl5). Elles ont un axe de symétrie
principal d'ordre supérieur à 2, c'est
à dire qu'elles sont inchangées lors d'une
rotation autour de cet axe de
360º / N, avec
N > 2. Les deux moments d'inertie
égaux sont perpendiculaires à cet axe de
symétrie; leur valeur est justement appelée
moment d'inertie perpendiculaire, notée
Iperp, alors que l'autre est le
moment d'inertie parallèle, noté
Ipar (ces moments sont
équivalents, respectivement, aux moments
IB et IA
définis plus haut).
|
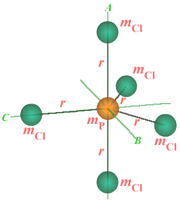 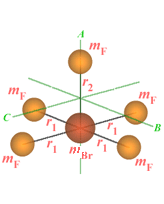 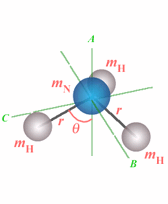
|
|
A : PCl5
|
B : BrF5
|
C : NH3
|
Figure 6.3.
Molécules de type toupie symétrique.
Pour les molécules du type
PCl5, l'atome de phosphore est au centre d'un
triangle constitué de trois atomes de chlore, les
deux autres étant directement au-dessus et
au-dessous de l'atome de phosphore (figure 6.3A).
Les moments d'inertie sont donnés
simplement par :
Ipar
= 3 mCl r2
Iperp
=
3/2 mCl r2
+ 2 mCl r'
2
Comme les longueurs
r et r' sont voisines, on peut faire
l'approximation suivante :
Iperp
= 7/2 mCl r2
Pour les molécules du type
BrF5, l’atome de brome est au centre d’un
carré constitué de quatre atomes de fluor
situés à une distance
r1 de l'atome de brome, le
cinquième atome de fluor étant directement
au-dessus de celui-ci, à une distance
r2 (figure 6.3B). Les
formules sont dans ce cas un peu plus
complexes :
Ipar
= 4
mF r12
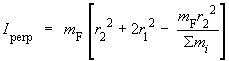
Σmi est la somme
des masses des atomes, soit
mBr + 5 mF.
Finalement, pour une molécule comme
NH3 (figure 6.3C), les expressions des moments
d'inertie sont :
Ipar = 3 mH r2
sin2 θ
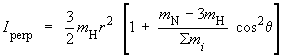
θ est l'angle entre la
liaison NH et l'axe de symétrie; il est
relié à l'angle entre deux liaisons NH,
noté HNH, par la relation suivante :
sin2 θ = 2/3
(1 – cos HNH)
Mentionnons que les molécules
planaires dotées d'un symétrie d'ordre
N > 2, NO3 par exemple,
sont aussi des toupies symétriques; certaines
constituent des cas particuliers des exemples
décrits ci-dessus. Ainsi, le cas de NO3
se ramène à celui de NH3 avec
θ = 90°.
Il faut aussi ajouter que certaines
molécules et certains radicaux diatomiques font
aussi partie des molécules de type toupie
symétrique. Considérons par exemple une
molécule telle que NO, qui possède un
électron non apparié. Dans ce cas le nuage
électronique n'a pas une symétrie
complètement cylindrique. Il y a un mouvement
très rapide des électrons autour de l'axe
internucléaire. Le moment d'inertie des
électrons est petit. Cependant, à cause de
leur mouvement très rapide en comparaison de celui
de chaque noyau, le vecteur moment cinétique le
long de l'axe A est comparable en grandeur
à celui le long des axes B et
C.
Niveaux d'énergie des
molécules spatiales
- Molécules de type sphérique
Les molécules de type
sphérique se traitent exactement de la même
manière que les molécules diatomiques. Il
n'y a qu'une seule constante rotationnelle B et le
terme spectral est donné par :
F(J) = BJ
(J+1) – DJ 2 (J+1)2
D est la constante de distorsion
centrifuge.
Le tableau 6.4 montre certains
résultats numériques relatifs à des
molécules de ce type.
Tableau 6.4.
Constantes de rotation
de quelques molécules de type
sphérique.
|
Molécule
|
B (cm–1)
|
D (cm–1)
|
|
CH4
|
5,239 ± 0,002
|
1,05 ± 0,03 × 10–4
|
|
CF4
|
0,191 134 ± 0,000 017
|
4,7 ± 0,6 × 10–8
|
|
SF6
|
0,091 11 ± 0,000 05
|
0,16
± 0,08 × 10–7
|
- Molécules de type toupie symétrique
L'introduction de deux moments d'inertie
distincts dans l'équation équation de
Schrödinger conduit à la définition de
deux nombres quantiques. Comme pour la spectroscopie
micro-ondes (module 1),
il est commode de garder le nombre quantique J
pour représenter le moment cinétique total
(vecteur P). On ajoute un nombre quantique
K pour le moment cinétique associé
à la rotation selon l'axe de symétrie de la
molécule (vecteur K).
La combinaison vectorielle de ces moments
cinétiques s'écrit :
P = M + K avec
| P | > | K |
Le vecteur M est le moment
cinétique associé à la rotation
selon un axe perpendiculaire à l'axe de
symétrie; aucun nombre quantique ne lui est
associé.
Ces vecteurs apparaissent sur l'animation
de la figure 6.4 qui permet d'explorer, pour la
molécule CH3Cl, le lien entre les
nombres quantiques J et K, le mouvement de
la molécule et les vecteurs M, K et
P.
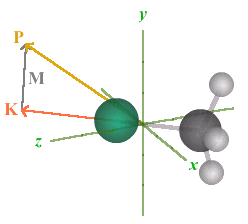
[ animation
]
Figure 6.4. Exploration de la rotation
d'une toupie symétrique : la molécule
CH3Cl.
La condition
| P | > | K |
implique que
J (J+1) > K 2 :
la valeur de J est nécessairement plus
grande ou égale à K, ou encore la
valeur de K est inférieure ou égale
à J. En général, pour une
valeur du moment cinétique total J, on voit
que K peut prendre les valeurs
suivantes :
K =
J, J–1, J–2, &, 0 ,
&, – (J–1), –J
Les valeurs négatives et positives
de K correspondent au fait que la molécule
peut tourner autour de son axe principal dans le sens
direct ou dans le sens inverse. Il existe donc pour un
niveau J, 2J + 1 valeurs de
K. On dira que le niveau J est
2 J + 1 fois
dégénéré.
En posant ω comme la valeur
de la vitesse angulaire (voir module 1),
E = 1/2
IA ωA2 + 1/2
IB ωB2 + 1/2
IC ωC2
E
= 1/2 IA ωA2 + IB ωB2
puisque IB =
IC
et
(rappel : E
= P 2 / 2I)
E
= PA2 / (2
IA) + PB2 / IB
PA et
PB représentent les moments
cinétiques par rapport aux axes A et
B respectivement. Cependant,

PB2 + PC2
= 2
PB2 = M 2
(h/π)2
= [ J (J + 1) – K 2 ] (h/2π)2
Il s'ensuit que :
|
(6.2)
|
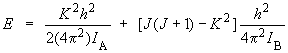
|
|
En se souvenant que F(J)
= E / hc, ces
valeurs étant exprimées en cm–1,
on peut écrire :
|
(6.3)
|
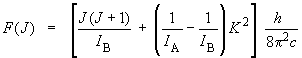
|
|
Si l'on pose :
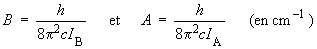
on obtient, en substituant ces expressions
dans l'équation précédente, le terme
spectral :
|
(6.4)
|
F(J,
K) = BJ (J + 1)
+ (A – B)
K 2 (cm–1).
|
|
Les toupies symétriques se
subdivisent en deux groupes selon que le moment d'inertie
IA (ou Ipar), relatif
à l'axe de symétrie de la molécule,
est plus petit ou plus grand que le moment d'inertie
IB (ou Iperp) :
- Les toupies symétriques
prolates (ou oblongues, à la
manière d'une ballon de rugby ou de football
américain): IA < IB;
- Les toupies symétriques
oblates (ou aplaties, à la
manière d'un palet de curling) :
IA > IB.
Pour les toupies symétriques
prolates, A est plus grand que B puisque
IA est plus petit que
IB. Le coefficient de
K2 dans l'équation 6.4,
soit la différence A – B,
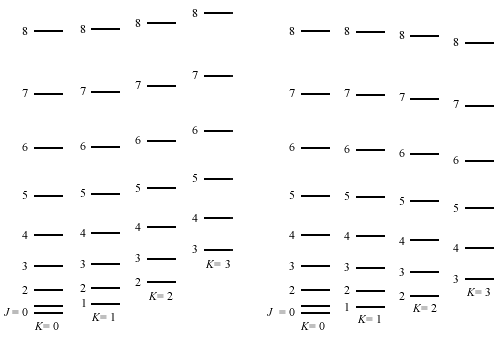
est alors positif. Il en découle que les
séries (verticales) de niveaux J
associés à une même valeur de
K seront déplacées en bloc vers le
haut (figure 6.5A), d'une quantité croissant
avec la valeur de K. Au contraire, pour les
toupies oblates, la différence A – B
est négative. Les séries de niveaux
J seront donc cette fois décalées
vers le bas (figure 6.5B).
On remarquera également dans la
figure l'absence, dans toutes les séries, de
niveaux avec J plus petit que K.
|
|
|
A : toupie
symétrique prolate
|
B : toupie
symétrique oblate
|
Figure 6.5.
Positionnement relatif des niveaux d'énergie
des molécules de type toupie symétrique
prolates et oblates.
Le spectre des molécules non
linéaires
- Toupies de type sphérique
En vertu de leur symétrie, les
molécules de type sphérique, à
l'instar des molécules diatomiques
homonucléaires (voir module 1),
ne possèdent pas de moment dipolaire permanent.
Puisque la variation de ce dernier constitue une
condition nécessaire à l'existence de
transitions rotationnelles, et par conséquent
à la manifestation d'un spectre dans la
région des micro-ondes, ces molécules ne
devraient présenter de tel spectre.
En réalité, les choses sont
un peu plus complexes. En effet, examinons le cas du
méthane, plus particulièrement la rotation
de la molécule autour d'une liaison C-H. Dans
l'hypothèse du rotateur rigide, la molécule
ne devrait pas montrer de spectre d'absorption
rotationnel. Cependant, la molécule n'étant
pas rigide, les angles HCH s'ouvrent quelque peu sous
l'effet de la force centrifuge, ce qui brise la
symétrie de la molécule et fait
apparaître un léger moment dipolaire. On
observe ainsi un spectre de faible intensité, mais
suffisant pour une analyse complète.
Par contre, pour une molécule comme
SF6, la déformation centrifuge ne
change pas la symétrie de la molécule. Il
n'y a donc pas apparition de moment dipolaire et, par
conséquent, pas de spectre micro-onde pour des
molécules de ce type.
- Toupies symétriques - hypothèse du
rotateur rigide
Par rapport aux molécules
diatomiques et sphériques, les règles de
sélection sont modifiées : on a
maintenant ΔJ = 0,
±1, et il existe une règle qui gouverne les
variations de K, soit ΔK = 0.
En effet, bien que la somme K + M
peut ne pas varier, les vecteurs K et M
peuvent varier de manière
indépendante.
Si on suppose que la molécule ne se
déforme pas lors de la rotation, la
différence d'énergie entre deux niveaux
d'énergie de rotation est donc donnée
par :
Δ = F(J+1,K) – F(J,
K) = B (J+1)(J+2) + (A–B) K 2
– [BJ (J+1) + (A–B) K 2] = F(J+1,K) – F(J,
K) = B (J+1)(J+2) + (A–B) K 2
– [BJ (J+1) + (A–B) K 2]
Δ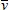 = 2
B (J + 1) = 2
B (J + 1)
Dans le spectre de vibration-rotation, on
va observer trois branches appelées P, Q et R
correspondant respectivement à ΔJ = –1,
0 et +1 (figure 6.6).
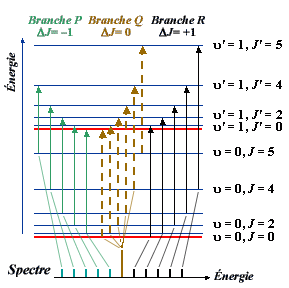
Figure 6.6. Transitions permises et spectre de
vibration-rotation théorique
d'une toupie symétrique.
Plus précisément :
- Lorsque ΔJ = –1, on a
la branche P (pauvre).
- Lorsque ΔJ = 0, on obtient
la branche Q, cette branche n'apparaissant que dans
une transition combinée vibration-rotation,
puisqu'en rotation pure, la transition est
évidemment nulle.
- Lorsque ΔJ = +1, la branche
R (riche) apparaît.
En vibration-rotation, le spectre sera
donc semblable à celui des molécules
diatomiques, à ceci près que pour la valeur
ΔJ = 0, on obtient une raie unique qui est en
fait la superposition des transitions J′ → J (0' → 0,
1' → 1, 2' → 2,
3' → 3, ... ). On obtient le
spectre théorique qui apparaît en bas de la
figure 6.6. Le spectre réel, qui comprend les
intensités des raies observées, se trouve
à la figure 6.7. On note que toutes les
transitions de la branche Q possèdent la
même énergie. Sur le spectre, la
superposition des ces raies produit une raie unique plus
intense que n'importe quelle autre raie. Ces observations
expérimentales permettent d'obtenir les valeurs de
la constante de rotation B (tableau 6.5).
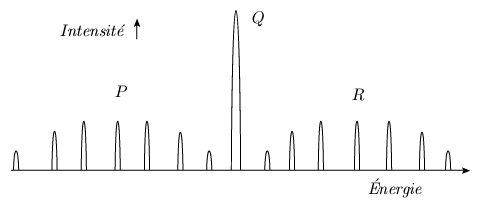
Figure 6.7. Spectre de vibration-rotation
d'une toupie symétrique.
Tableau 6.5. Quelques valeurs de constantes de
rotation
de molécules de type toupie symétrique.
|
Molécule
|
B(cm–1)
|
Molécule
|
B(cm–1)
|
|
CH3F
|
0,851 887
|
NH3
|
9,943 455
|
|
CH3Cl
|
0,443 546
|
CH3SiH3
|
0,366 005
|
|
(CH3)3P
|
0,194 072
|
(CH3)3CF
|
0,157 232
|
|
CCl3H
|
0,110 177
|
NF3
|
0,356395
|
|
Note :
On trouvera une longue liste de telles valeurs
dans
Lojko, M. S. et Y. Beeres. J. Res. Nat.
Bureau Stand., Sect. A (1969),
73A(2), 233-239.
|
Par contre, avec un
spectromètre basse résolution, comme
ceux habituellement utilisés dans un laboratoire
d'analyse, le même spectre est
« compressé », de telle sorte
que l'on ne voit que l'enveloppe des raies
(figure 6.8; voir aussi module 2, figure
2.2).
Figure 6.8. Spectre de vibration-rotation
théorique
d'une toupie symétrique
sous basse résolution.
Dans le cas des spectres
électroniques, on retrouve la parabole de Fortrat
qui systématise les raies des branches P et R. On
obtient également une branche Q, qui forme un
morceau d'une autre parabole. En effet, compte tenu des
différences parfois importantes entre les
distances internucléaires des divers états
électroniques, les constantes de rotation sont
différentes, ce qui entraîne une
différence d'énergie pour une même
valeur de J. Par conséquent, les
transitions, donc les raies, pour lesquelles ΔJ = 0
n'ont plus la même valeur.
L'énergie (en unités de
nombre d'ondes) d'un niveau de rotation-vibration
quelconque dans un état électronique
excité est telle que :
E' = Eélec
+ F(J′) + G(υ') = Eélec
+ B′J′ (J′ + 1) +
(A' – B′) K2
+ G(υ')
et pour un niveau de l'état
électronique fondamental :
E = F(J)
+ G(υ) = BJ (J + 1)
+ (A – B) K2
+ G(υ)
On admet, en effet, que le terme
(A – B) K2
a la même valeur dans les deux états. En
incluant la différence G(υ') – G(υ)
dans le premier terme 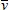 00,
on obtient : 00,
on obtient :
|
(6.5)
|
R(J) =
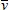 00
+ B′ (J+1)(J+2) – BJ (J+1), ΔJ
= +1 00
+ B′ (J+1)(J+2) – BJ (J+1), ΔJ
= +1
Q(J) = 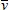 00
+ B′J (J+1) – BJ (J+1), ΔJ
= 0 00
+ B′J (J+1) – BJ (J+1), ΔJ
= 0
P(J) = 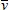 00
+ B′J (J–1) – BJ (J+1), ΔJ
= –1 00
+ B′J (J–1) – BJ (J+1), ΔJ
= –1
|
|
En appliquant le changement de variable
approprié, soit m = –J
pour la branche P, m = J pour la
branche Q et m = J + 1
pour la branche R, les deux séries de raies
correspondantes sont comprises dans la parabole de
Fortrat. Il faut se rappeler qu'il manque un certain
nombre de raies puisque J > N,
ou N est le moment cinétique
électronique et si N = n,
J > n. Pour indexer les raies
convenablement on peut utiliser la méthode de la
seconde différence (voir module 3)
ou encore celle de la combinaison de
différences.
On
a : Δ1F(J)
= R(J) –
Q(J) = Q(J+1)
– P(J+1)
et : Δ1F(J) = R(J)
– Q(J+1) = Q(J)
– P(J+1)
En effet, en ignorant la valeur de 00, qui
s'annule dans les soustractions, on obtient :
R(J) –
Q(J) = B′ (J+1) (J+2)
– BJ (J+1) – B′J (J+1)
+
BJ (J+1) = 2B′J (J+1)
Q(J+1)
– P(J+1)
= B′ (J+1)(J+2) – B (J+1)(J+2)
– B′J (J+1) +
B (J+1)(J+2)
Q(J+1) – P(J+1)
= 2B′J (J+1)
De la même manière, on
montrerait que :
R(J) – Q(J+1) =
Q(J) – P(J+1) = 2B′J (J+1) = Δ1F(J)
On obtient donc dans tous les cas la
même expression pour la première
différence :
|
(6.6)
|
Δ1F(J) = 2
B′ (J+1)
|
|
Note : Δ1F(J)
mesure la différence d'énergie pour des
raies de même J dans deux branches
différentes.
- Toupies symétriques - hypothèse du
rotateur non rigide
L'équation
6.4 s'applique à un rotateur rigide. On doit
se demander ce qu'il advient dans l'hypothèse
très probablement plus réaliste où
le rotateur n'est plus rigide. Lorsqu'on tient compte de
la force centrifuge, la solution de l'équation de
Schrödinger fait apparaître trois termes
correctifs. L'énergie d'un niveau de rotation (en
cm–1) est alors donnée
par :
|
(6.7)
|
F(J, K) = BJ (J+1)
+ (A – B)
K 2 – DJ J 2(J+1)2 – DJK J (J+1) K 2 – DK K 4
|
|
Les trois termes correctifs sont toujours
très petits devant les constantes A et
B. Le premier avec le coefficient
DJ correspond à la correction
due à la force centrifuge : c'est la
même correction introduite pour la rotation des
molécules diatomiques
héteronucléaires (module 1).
Il correspond à la non-rigidité de la
molécule selon l'axe de rotation perpendiculaire
à l'axe de symétrie de la
molécule.
La présence des deux autres termes
correctifs, DJK et
DK, est moins évidente.
L'exemple de la molécule CH3Cl permet
de mieux comprendre leur pertinence. En effet, la force
centrifuge due à la rotation autour de l'axe de
symétrie a deux effets : elle augmente la
longueur de la liaison C–H et elle rend les angles
H–C–Cl davantage perpendiculaires à la
liaison, ce qui dans les deux cas augmente le moment
d'inertie. Ces effets sont, bien sûr, d'autant plus
importants que la vitesse de rotation est grande. La
figure 6.9 permet de visualiser (à
défaut d'en faire la démonstration) le
rationnel de ces corrections dues à la force
centrifuge.
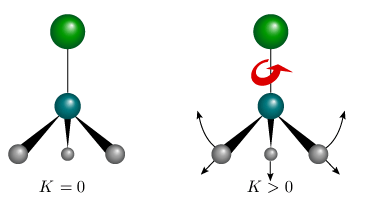
Figure 6.9. Effet de la force centrifuge sur la rotation
d'une toupie symétrique
selon son axe de symétrie : cas de
CH3Cl.
La différence d'énergie
entre deux niveaux d'énergie de rotation est
maintenant donnée par :
|
(6.8)
|
Δ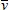 = F(J+1,K)
–
F(J,K) = 2B (J+1)
–
4 DJ (J+1)3 –
2 DJK (J+1)K 2 = F(J+1,K)
–
F(J,K) = 2B (J+1)
–
4 DJ (J+1)3 –
2 DJK (J+1)K 2
|
|
Étant donné que pour chaque
valeur de J, K peut prendre
2J = 1 valeurs, chaque transition sera
dédoublée. Comme le terme K
apparaît au carré, au lieu d'observer un
dédoublement en 2J + 1 raies, on
n'observera que J + 1 raies pour chaque
valeur de J. Le tableau 6.6 montre les
valeurs des transitions rotationnelles théoriques
ainsi qu'un cas d'espèce : celui de
CH3F.
Tableau 6.6. Effet
des termes de correction sur les transitions d'une toupie
symétrique.
|
Niveau d'origine
|
Énergie de la transition (cm–1)
|
|
J
|
K
|
F(J+1, K) –
F(J, K)
|
Valeurs pour CH3F*
|
|
0
|
0
|
4B –
4 DJ
|
--
|
|
1
|
0
|
4B – 32
DJ
|
3,404 752
|
|
1
|
4B – 32
DJ – 4
DJK
|
3,404 693
|
|
2
|
0
|
6B – 108
DJ
|
5,107 008
|
|
1
|
6B – 108
DJ – 6
DJK
|
5,106 920
|
|
2
|
6B – 108
DJ – 24
DJK
|
5,106 655
|
|
*
Tiré de Banwell, C. N. Fundamentals of
Molecular Spectroscopy,
McGraw-Hill Book Company (UK) Limited,
2e édition, 1972.
|
Le tableau 6.7 donne, pour quelques
molécules, les valeurs des constantes
nécessaires au calcul précis des
transitions rotationnelles de molécules de type
toupie symétrique.
Tableau 6.7.
Constantes de rotation de molécules de type toupie
symétrique,
incluant les termes de correction.
|
Molécules
|
B (cm–1)
|
DJ (cm–1)
|
DJK (cm–1)
|
réf.
|
|
NH3
|
9,9439
|
0,197 × 10–3
|
– 3,50 × 10–3
|
a
|
|
ND3
|
5,1426
|
0,197 × 10–3
|
– 3,52 × 10–3
|
a
|
|
15NH3
|
9,9197
|
|
|
a
|
|
NF3
|
0,3563
|
0,484 × 10–6
|
– 0,756 × 10–6
|
b
|
|
a.
Helminger, P., F. C. De Lucia et W. Gordy, J.
Mol. Spectrosc., 39(1), 94-97 (1971).
b. Mirri, A. M. et G. Cazzoli, J. Chem.
Phys., 47(3), 1197-1198 (1967).
|
On note que dans ces exemples :
- les ordres de grandeurs diminuent de
manière importante quand on passe de B
aux constantes D;
- la substitution isotopique de l'hydrogène
par le deutérium affecte de manière
importante la constante de rotation B, mais peu
les constantes DJ et
DJK.
Le spectre de rotation type d'une telle
molécule, décrit par l'équation 6.8,
apparaît dans la figure 6.10. Pour rendre
compréhensible le spectre, on a
délibérément exagéré
les espaces entre les raies correspondant à la
même valeur de J et différentes
valeurs de K. On se rappellera en outre que chaque
raie J, K est double sauf la raie correspondant
à la valeur K = 0.
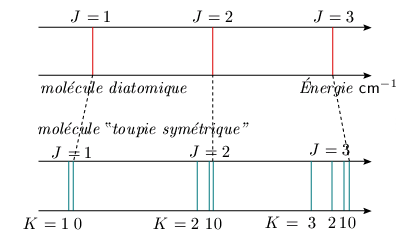
Figure 6.10. Comparaison entre les spectres
schématiques de rotation
d'une molécule diatomique et d'une molécule
de type toupie symétrique.
Il faut ajouter que les molécules
de type toupie symétrique qui n'ont pas de moment
dipolaire, comme le benzène, ne présentent
pas de spectre de rotation. Notons que dans ce cas,
contrairement à ce qu'on a vu plus haut pour le
méthane décrit, la force centrifuge, quel
que soit l'axe de rotation considéré,
n'introduit pas de moment dipolaire.
- Molécules de type toupie asymétrique
Une molécule de type toupie
asymétrique possède trois moments d'inertie
différents. Les niveaux d'énergie de
rotation d'une telle molécule ne peuvent plus
être représentés par une seule
équation en fonction de ses moments d'inertie.
Plusieurs nombres quantiques entrent en jeu,
dépendant de chacun des moments d'inertie. Le
spectre devient très compliqué et chaque
molécule constitue un problème
indépendant.
La structure des molécules non
linéaires
- Molécules de type toupie
symétrique
On peut donc obtenir pour n'importe quelle
molécule de type toupie symétrique la
valeur de la constante de rotation B
(tableau 6.5) et donc la valeur de son moment
d'inertie IB. Bien entendu, pour une
molécule diatomique appartenant à ce
groupe, comme NO, on obtient facilement la longueur de la
liaison. Pour une molécule polyatomique, les
paramètres moléculaires sont
déterminés à l'aide de
molécules isotopiques. Ces paramètres
comprennent non seulement les distances
internucléaires, mais également les angles
entre les liaisons. Le tableau 6.8 présente
plusieurs de ces caractéristiques
géométriques obtenues à partir des
spectres de rotation de toupies symétriques.
Tableau 6.8.
Paramètres géométriques
de quelques molécules non linéaires
de type toupie symétrique.
|
Molécules
|
Angles entre
les liaisons
|
Longueurs de liaison
re (nm)
|
Longueurs de liaison
re (nm)
|
|
CH3F
|
HCH 110º0'
|
C–H
0,1109
|
C–F
0,1385
|
|
CH3CºN
|
HCH 109º8'
|
C–H 0,1092
|
C–C
0,1460
|
|
CºN
0,1158
|
|
|
CHCl3
|
ClCCl 110º24'
|
C–H
0,1073
|
C–Cl 0,1767
|
|
SiH3Br
|
HSiH 111º20'
|
Si–H
0,157
|
Si–Br
0,2209
|
|
PCl3
|
ClPCl
100º6'
|
P–Cl 0,2043
|
|
|
SbH3
|
HSbH 91º30'
|
Sb–H 0,1712
|
|
|
PH3
|
HPH 93º18'
|
P–H 0,144
|
|
|
NH3
|
HNH 107º18'
|
N–H
0,1008
|
|
- Molécules de type toupie asymétrique
En dépit de la complexité de
leur spectre, on a pu déterminer par analyse de
spectre les paramètres géométriques
de quelques molécules asymétriques
relativement simples. Le tableau 6.9 en
présente quelques exemples.
Tableau 6.9.
Données numériques sur les
paramètres géométriques
de quelques molécules de type toupie
asymétrique.
|
Molécules
|
Angles entre les liaisons
|
Longueurs
de liaison
re (nm)
|
Longueurs
de liaison
re (nm)
|
|
H2O
|
HOH 104º31'
|
O–H 0,09572
|
|
|
HN=C=O
|
HNC 128º5'
|
H–N 0,0987
|
N=C 0,1207
|
|
NCO (180)
|
C=O 0,1171
|
|
|
CH2Cl2
|
HCH 112º0'
|
C–H 0,1068
|
C–Cl 0,17724
|
|
ClCCl 111º47'
|
|
|
|
SO2F2
|
OSO 129º38'
|
S=O 0,1370
|
S–F 0,1570
|
|
FSF 92º47'
|
|
|
|
O3
|
OOO 116º49'
|
O–O 0,1278
|
|
|
CH3SC'ºN
|
HCH (109º)
|
C–H 0,109
|
C–S 0,181
|
|
CSC' 142º
|
C'ºN 0,121
|
C'–S 0,161
|
|
CH3OH
|
HCH (109º28')
|
C–H 0,110
|
C–O 0,1421
|
|
COH 110º15'
|
O–H 0,0958
|
|
|
Note :
Les valeurs entre parenthèses sont
incertaines.
|
Effet Stark sur les transitions de
rotation
Pour qu'il y ait transition de rotation, il
faut qu'il y ait variation du moment dipolaire durant le
saut en rotation. On peut donc se demander quelle sera
l'influence d'un champ électrique sur chacun des
niveaux rotationnels, et donc sur les transitions.
Sans entrer dans le détail, mais de
façon similaire à l'effet
Zeeman sur les niveaux énergétiques de
l'atome, un rotateur de nombre quantique J (nombre
quantique associé au moment cinétique
P), possède 2J + 1
façons de s'orienter dans le champ électrique.
Chacune de ces orientations peut être
caractérisée par un nombre quantique M,
proportionnel à la composante du moment
cinétique parallèle au champ, dont les valeurs
possibles vont de –J à +J. Ainsi,
pour les molécules linéaires et les toupies
sphériques, chaque niveau J, initialement
dégénéré (i.e. dont les
sous-niveaux ont tous la même énergie) va
être dédoublé en 2J + 1
sous-niveaux dont l'énergie varie selon chacune des
valeurs de M (figure 6.11). Ce
phénomène est appelé effet
Stark.
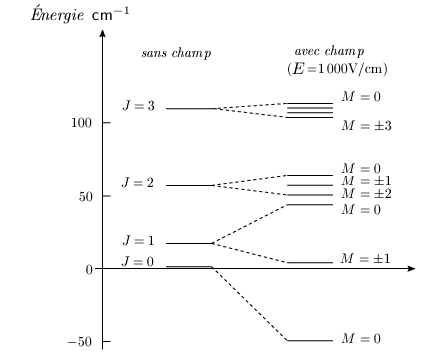
Figure 6.11. Effet Stark sur HCl.
Voir Barrow, G. M. Introduction to Molecular
Spectroscopy,
McGraw-Hill Book Company, Inc., New York 1962.
On montre que la variation d'énergie
de d'un niveau J est telle que :
|
(6.9a)
|
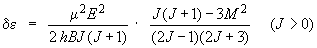
|
|
|
(6.9b)
|
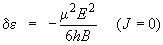
|
|
μ et B sont respectivement
le moment
dipolaire et la constante de rotation de la
molécule; E est la grandeur du champ
électrique appliqué.
À la règle de sélection ΔJ = ±1
toujours valide, il faut ajouter ΔM = 0,
car il ne peut y avoir de variation de l'orientation du
dipôle dans le champ électrique au cours de la
transition. On voit donc que l'énergie des raies est
affectée proportionnellement au facteur (μE)2.
Pour les molécules de type toupie
symétrique, le mécanisme d'interaction entre
μ et E est plus complexe. L'énergie
des raies est affectée par le facteur μE.
Dans les deux cas, la variation de δε
en fonction de E permet d'obtenir des valeurs
précises de μ (tableau 6.10).
Il faut enfin mentionner que le champ
électrique peut provenir du spin nucléaire
I des noyaux atomiques. Il y a alors une structure de
raies rotationnelles appelée structure
hyperfine.
Tableau 6.10.
Longueurs de liaisons et moments dipolaires obtenus par
effet Stark.
|
Molécules
|
Type
|
Longueurs de liaison
re (nm)
|
Moment dipolaire
(Debye)
|
|
Na–Cl
|
linéaire
|
Na–Cl : 0,23606
|
8,5 ± 0,2
|
|
O=C=S
|
linéaire
|
C=O : 0,1164
|
0,712 ± 0,004
|
|
C=S : 0,1559
|
|
H–CºN
|
linéaire
|
C–H : 0,10632
|
2,986 ± 0,004
|
|
CºN : 0,11553
|
|
NH3
|
toupie symétrique
|
N–H : 0,1008
|
1,47 ± 0,01
|
|
CH3–Cl
|
toupie symétrique
|
C–H : 0,10969
|
1,871 ± 0,005
|
|
C–Cl : 0,17812
|
|
D'après Banwell,
C. N. Fundamental of Molecular Spectroscopy,
2e édition, McGraw-Hill Book
Company Ltd., London, 1972.
|
Conclusions
L'application de la mécanique
quantique est toujours féconde pour
l'interprétation des observations spectroscopiques du
mouvement de rotation des molécules polyatomiques. On
obtient non seulement les longueurs de liaison mais
également les angles entre les liaisons. Les
règles de sélection et les lois qui gouvernent
ces processus sont conservées. La variation de moment
dipolaire est la variable déterminante qui
établit la faisabilité d'une transition.
L'application d'un champ électrique
intense permet de lever la
dégénérescence des niveaux et donc
d'observer le dédoublement des raies en rotation.
Pour en savoir plus
Hollas, J. M., Basic Atomic and Molecular
Spectroscopy, Wiley-Interscience, 2002.
Herzberg, G. Molecular Spectra and
Molecular Structure II Infrared and Raman Spectra of
Polyatomic Molecules, D. van Nostrand Comp. Inc.,
Princeton, New Jersey, 1968.
NSRDS-NBS 39, Tables of Molecular
Vibrational Frequencies (consolidated vol. 1), 1972.
Banwell, C. N. Fundamentals of Molecular
Spectroscopy, 2nd edition, McGraw-Hill Book
Company (UK) Limited, 1972.
Valeur des constantes de rotation :
Lojko, M. S. et Y. Beeres. J. Res. Nat. Bureau Stand.,
Sect. A (1969), 73A(2), 233-239.
Liens utiles
Plusieurs structures de molécules
simples peuvent être retrouvées sur le site Web
(en français ou en anglais) du Lycée
Faidherbe, Lille (France). Basée sur la thééorie de répulsion des électrons de la couche de valence (VSEPR de Valence Shell Electron Pair Repulsion) développée par le professeur R.J Gillespie (université Mc Master, Hamilton, Ontario), on y trouvera en plus des molécules que l'on peut manipuler, les longueurs et les angles de liaison. http://www.faidherbe.org/site/cours/dupuis/vsepr.htm
Les biographies de Pieter Zeeman et de
Johannes Stark ainsi que d'autres éléments
sont disponibles sur le site des Prix Nobel :
http://www.nobel.se/physics/laureates/1902/zeeman-bio.html
http://www.nobel.se/physics/laureates/1919/stark-bio.html
Par ailleurs, le site Web de la Georgia State
University présente des diapos intéressantes
relativement à l'effet Zeeman, au facteur de
Landé et à beaucoup d'autres
choses. Ce site, qui peut aussi être
avantageusement utilisé comme glossaire à
travers son index, a été construit par Carl R.
(Rod) Nave :
http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html
|



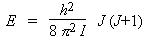
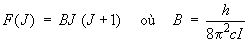

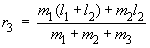
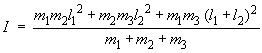





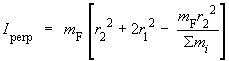
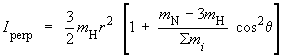


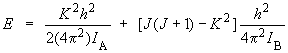
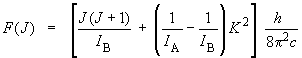
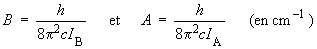

 = F(J+1,K) – F(J,
K) = B (J+1)(J+2) + (A–B) K 2
– [BJ (J+1) + (A–B) K 2]
= F(J+1,K) – F(J,
K) = B (J+1)(J+2) + (A–B) K 2
– [BJ (J+1) + (A–B) K 2]