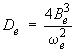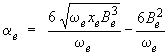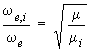|
|
|
|
MODULE 3 Vibration-rotation
des molécules diatomiques Préambule La molécule diatomique, la plus simple, tourne sur elle-même et vibre le long de sa liaison interatomique. Comment la combinaison de ces deux mouvements se traduit-elle dans le spectre d'absorption d'une molécule? Comment doit-on combiner les nombres quantiques associés à la rotation et à la vibration? Par ailleurs, comment se traduit, dans les spectres observés et leur description mathématique, la présence d'isotopes dans la molécule?
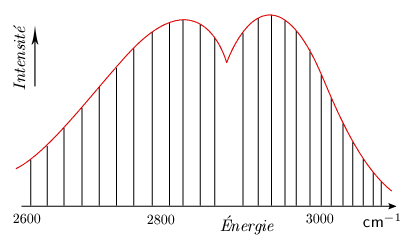
Faits expérimentaux Si l'on examine les bandes d'absorption du proche infrarouge (1 à 5 μm) à l'aide d'un instrument à dispersion élevée, on constate que la bande unique (mais large) se résout en un certain nombre de raies. Ces raies se divisent en deux groupes (ou branches) de raies, dont l'intervalle diminue légèrement avec la fréquence, entre lesquels se trouve un intervalle plus large, double de l'intervalle qui sépare les raies. Non seulement la bande fondamentale, mais également les harmoniques possèdent une telle structure, caractérisée par une raie manquante au centre de la bande (figure 3.1).
La répartition de l'intensité de ces raies dans chaque branche est très caractéristique. Chaque branche possède un maximum d'intensité. De part et d'autre de ce maximum, l'intensité des raies décroît régulièrement. On constate que la position de ce maximum varie avec la température (le maximum s'écarte de la raie manquante lorsque la température croît). Les fréquences de ces raies peuvent se représenter, en première approximation, par une formule du type :
a est la même constante que dans le spectre de rotation pure (voir module 1); b est une constante approximativement égale à la constante b introduite à propos des spectres de vibration pure (module 2); m est un nombre entier positif. Cette formule simple prévoit des niveaux également espacés. La diminution de l'intervalle entre les raies successives, bien visible dans le spectre de la figure 3.2, peut être représentée, comme on le verra plus loin, par l'ajout de termes de correction contenant des puissances de m plus élevées.
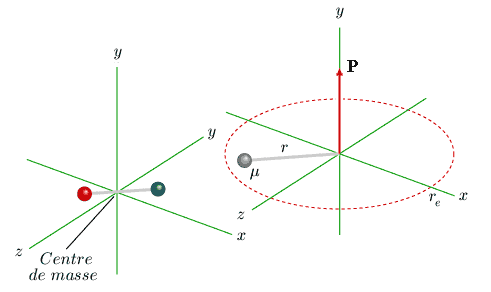
Modèle mécanique - l'oscillateur tournant Le modèle le plus simple pouvant représenter la rotation et la vibration d'une molécule autour de son centre de masse est l'oscillateur harmonique tournant (ou rotateur vibrant). Un tel oscillateur est défini comme un point de masse μ, appelée masse réduite, tournant à une distance r autour d'un axe de rotation fixe. Cette distance r n'est pas constante, mais oscille autour d'une valeur re appelée position d'équilibre (figure 3.2). Cette oscillation est due à une force de rappel proportionnelle au déplacement par rapport à cette position d'équilibre.
[ Une animation est disponible
] L'énergie d'un oscillateur tournant est donnée par la somme des énergies associées à chaque mouvement, soit : E = Erotation + Eoscillation = 1/2 I ω2 + 1/2 kA2 I est le moment d'inertie, égal à 1/2 μre2, k la constante de rappel (qui décrit la rigidité de la liaison) et A l'amplitude de l'oscillation.
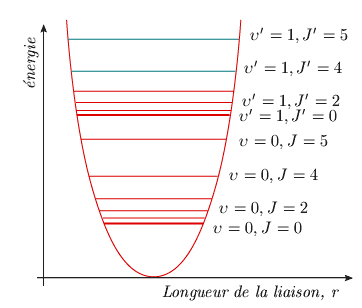
Modèle quantique Selon la mécanique quantique, l'énergie d'un objet ou d'un système confiné (c'est-à-dire dont la position est limitée à un domaine fini), ou encore soumis à des conditions périodiques, ne peut prendre que certaines valeurs prédéfinies. Ces valeurs discrètes, appelées niveaux d'énergie, sont reliées à des nombres entiers, les nombres quantiques υ et J, associés respectivement à la vibration et à la rotation. En règle générale, une molécule possédera les deux mouvements à la fois. On peut admettre, en première approximation du moins, que ces deux mouvements sont indépendants. Cette simplification permet de supposer que les états d'énergie du système sont simplement la superposition des états d'énergie correspondant à la rotation et à la vibration. Dans ces conditions, comme pour le modèle classique de l'oscillateur tournant, l'énergie de la molécule sera égale à la somme des énergies associées à la vibration et à la rotation. Supposons tout d'abord la molécule dans l'état de vibration fondamental, soit υ = 0. Si elle ne tourne pas, son énergie cinétique de rotation est nulle et correspond donc au niveau de rotation J = 0. L'énergie totale est donc celle du niveau υ = 0. Sans changer de mode de vibration, la molécule peut changer d'énergie de rotation. Elle passera successivement aux niveaux J = 1, 2, 3, ... Ce raisonnement peut être généralisé aux autres niveaux de vibration υ = 1, 2, 3, .... Au-dessus de chacun des niveaux de vibration, on trouve une série de niveaux de rotation (figure 3.3).
Figure 3.3. Niveaux d'énergie de vibration et de rotation.
On constate que les niveaux de vibration sont assez éloignés les uns des autres (séparation ωe) et à peu près équidistants. De leur côté, les niveaux de rotation, dont la séparation est égale à 2B (J + 1), sont plus rapprochés et s'écartent les uns des autres à mesure que J augmente, c'est-à-dire à mesure que l'énergie cinétique de rotation croît. Dans certaines conditions, il est d'ailleurs possible que les niveaux de rotation correspondant à un état de vibration dépassent le niveau de vibration suivant. Quantitativement, l'énergie d'un niveau caractérisé par les nombres quantiques υ et J sera donnée par :
Le terme spectral correspondant sera :
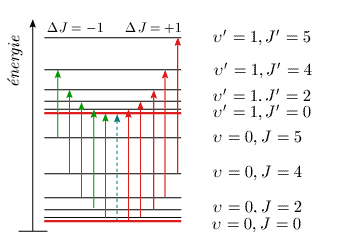
Le terme contenant D est associé à la distorsion centrifuge (voir module 1), alors que celui où apparaît ωexe est relié à l'anharmonicité de la vibration (module 2). Spectre de vibration-rotation Un résultat important de la mécanique quantique est que les transitions entre niveaux d'énergie ne sont pas toutes possibles, et que certaines, tout en étant possibles, sont beaucoup moins probables que d'autres. On démontre que les transitions possibles pour l'oscillateur tournant sont toujours : Δυ = ±1 avec grande probabilité Il est aisé de voir sur un diagramme l'allure que prendra dans ces conditions le diagramme des transitions de la bande fondamentale (figure 3.4). La raie manquante (flèche pointillée) correspond à la transition interdite J = 0 → J′ = 0.
L'énergie des transitions possibles peut être calculée à partir du terme spectral. Tout d'abord, pour une transition vibrationnelle du niveau υ = 0 au niveau υ = 1, on a : ΔG = G (υ = 1) – G (υ = 0) = ωe – 2 ωexe et ΔG représente la transition de vibration pure. Cette transition vibrationnelle pure υ = 0, J = 0 → υ' = 1, J′ = 0, interdite puisque ΔJ = 0, apparaît sous forme de pointillés dans la figure 3.4. Pour les transitions rotationnelles, il faut considérer deux possibilités. Pour simplifier on considère que les constantes B et D ont les mêmes valeurs dans les deux niveaux de vibration.
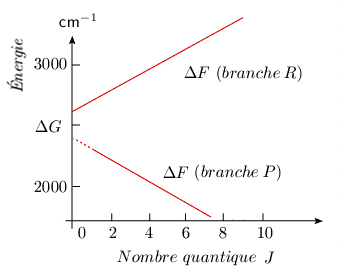
La figure 3.5 montre les deux courbes qui représentent l'énergie (égale à ΔG + ΔF) des deux séries de raies R et P de la bande fondamentale. On remarque qu'il s'agit pratiquement de droites, ce qui traduit le fait que D est beaucoup plus petit que B.
Interaction vibration-rotation On a, jusqu'à présent, traité les mouvements de rotation et de vibration de manière complètement indépendante. En fait, tel n'est pas le cas. La rotation et la vibration sont interreliées à divers points de vue, dont deux seront traités ici. Premièrement, l'énergie de rotation est influencée par le nombre quantique de vibration, phénomène appelé interaction vibration-rotation. Deuxièmement, des constantes rotationnelles comme la distorsion centrifuge peuvent être reliées mathématiquement à la fréquence de vibration.
Considérons d'abord l'interaction vibration-rotation. Au cours du mouvement de vibration, la distance interatomique change constamment, ce qui entraîne une variation du moment d'inertie de la molécule. Mais la période de vibration est en général beaucoup plus petite que celle de la rotation. En d'autres termes, la molécule effectue plusieurs vibrations pendant le temps requis pour effectuer une rotation. Dans l'expression du terme spectral (équation 3.2), on peut donc remplacer la valeur de la constante rotationnelle B par sa moyenne, notée Bυ, qui dépend du nombre quantique de vibration υ :
La ligne horizontale au-dessus du rapport 1/r2 signifie justement la valeur moyenne de ce rapport. Un calcul approprié, fondé sur la mécanique quantique, montre que la constante de rotation corrigée Bυ s'écrit : Bυ = Be – αe (υ + 1/2) + γe (υ + 1/2)2 + ... αe est une constante beaucoup plus petite que Be (la valeur non corrigée) et γe une constante encore plus faible. Cette correction est donc généralement peu importante; par exemple, pour la molécule HBr, on a : Bυ = 0 = 8,360 cm–1 et Bυ = 1 = 8,134 cm–1 De la même manière, la constante de distorsion centrifuge varie elle aussi avec le nombre quantique de vibration : Dυ = De – Δe (υ + 1/2) + ... Note : La constante De de cette formule ne doit pas être confondue avec l'énergie de dissociation spectroscopique (module 2), représentée par le même symbole. Cette dernière correction, encore moins importante que la précédente, est souvent négligée; d'ailleurs, elle n'est pas incluse dans la simulation VR Molécules. Le tableau 3.1 présente les valeurs de ces constantes de rotation pour quelques molécules diatomiques. Tableau 3.1. Constantes rotationnelles de quelques molécules diatomiques.
Relations entre les constantes moléculaires Le second type de lien entre la vibration et la rotation se manifeste par l'existence de relations mathématiques entre les constantes rotationnelles et la fréquence de vibration. Ces relations découlent de l'hypothèse du rotateur non rigide. En effet, tant la fréquence de vibration que l'allongement de la distance interatomique causé par la rotation (distorsion centrifuge) dépendent de la rigidité de la liaison interatomique, décrite par la constante de force, ou constante de rappel (voir module 2). Nous nous contenterons ici d'indiquer les résultats que fournit à ce propos la mécanique quantique. Tout d'abord, la constante de distorsion centrifuge peut être reliée à la constante de vibration ωe :
Cette relation traduit bien le fait que plus la fréquence de vibration est élevée, ce qui signifie une liaison plus rigide, moins la liaison s'allongera sous l'effet de la force centrifuge. Ensuite, un calcul approprié, hors des limites de ce module, fondé sur la courbe de potentiel de Morse (voir module 2) permet de relier la constante αe, qui décrit l'interaction vibration-rotation, à la fréquence de vibration :
Ici aussi une fréquence élevée, signe d'une liaison rigide, correspondra à une correction moins importante, l'amplitude de la vibration variant peu d'un nombre quantique de vibration à l'autre. Finalement, on peut reprendre les calculs ayant mené aux expressions des fréquences des raies des bandes R et P, cette fois en considérant le fait que la constante B n'est pas la même pour les deux niveaux de vibration. On négligera cependant la variation de la constante D, qui ajoute une correction encore plus faible. Si on note B′ et B" les valeurs de la constante B pour les niveaux de vibration inférieur et supérieur respectivement, on montre, en suivant les étapes qui ont mené aux équations 3.3 et 3.4, que le terme spectral de rotation ΔF s'écrit maintenant : (a) bande R : ΔF = (J+1) [ (J+2) B" – JB′ ] – 4 D (J+1)3 (b) bande P : ΔF = J [ (J–1) B" – (J+1) B′ ] + 4 DJ 3 Ces expressions analytiques différentes peuvent être combinées par un changement de variable approprié.
Les expressions analytiques des deux termes spectraux sont alors identiques, et le terme spectral général, incluant le terme de vibration, peut être réécrit sous la forme :
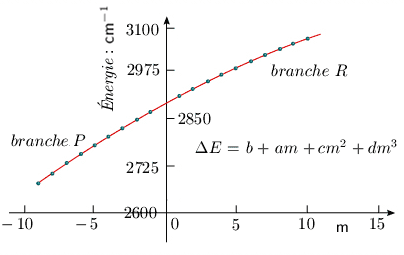
où b = ωe – 2 ωexe am = mB" + mB′ Þ a = B" + B′ cm2 = m2B" – m2B′ Þ c = B"– B′ et d = – 4D. La figure 3.6 illustre la courbe de l'énergie en fonction du paramètre m. La courbure peu prononcée indique encore une fois que les corrections, associées aux paramètres c et d, beaucoup plus petits (en valeur absolue) que a et b, sont relativement faibles.
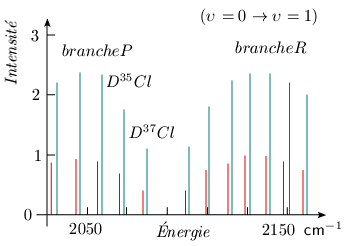
Remarque Effet isotopique Puisque la masse intervient dans la constante de rotation Be et dans la fréquence de vibration ωe, on peut prévoir que les fréquences d'absorption seront différentes pour une molécule normale et pour une molécule isotopique. On observe expérimentalement un tel déplacement des fréquences d'absorption lorsqu'il y a présence de molécules de compositions isotopiques différentes. Ainsi, la structure de vibration-rotation de DCl présente des raies d'absorption dédoublées correspondant au mélange naturel D35Cl, D37Cl. Dans ce cas, la variation de la masse réduite étant faible, le spectre est très peu déplacé (figure 3.7). Notez que, dans cette figure, les intensités relatives des raies de D35Cl et de D37Cl ne sont pas dans la proportion de l'abondance isotopique naturelle D35Cl / D37Cl (3/1). Les probabilités de transition (voir module 5) expliquent en partie cette absence de concordance; voir également à ce sujet le problème 6.
Par contre, pour deux molécules du type H35Cl et D35Cl, le facteur de variation de masse réduite est voisin de 2. En conséquence, les spectres sont alors situés dans des régions totalement différentes : H35Cl : bande
fondamentale à 3,46 μm. De manière générale, on peut prévoir quantitativement la position des niveaux d'énergie d'une molécule isotopique en calculant les constantes de la nouvelle molécule à partir des constantes de la molécule normale. Pour la rotation :
Be,i est la constante de rotation de la molécule isotopique.
ωe,i est la constante relative à la molécule isotopique. On peut montrer également que :
Conclusions Les deux mouvements de rotation et de vibration de la molécule s'ajoutent simplement. Chaque mouvement garde ses caractéristiques (niveaux d'énergie, nombres quantiques, règles de sélection). Il existe toutefois des liens entre ces deux mouvements, associés à la variation de la distance interatomique lors du mouvement de vibration. Ce phénomène rend les constantes de rotation légèrement dépendantes du nombre quantique de vibration, ce qui se traduit par l'ajout de termes de correction. Par ailleurs, l'effet sur ces mêmes constantes de la substitution d'un atome par un de ses isotopes peut aisément être déterminé à partir des valeurs des masses réduites des deux versions de la molécule.
Pour en savoir plus Herzberg, G. Molecular Spectra and Molecular Structure. I. Spectra of Diatomic Molecules. Van Nostrand Reinhold Company, Toronto, 1950, 658 pages. Pour la dépendance des constantes B et D avec le nombre quantique de vibration, voir : Pekeris, C. L. The rotation-vibration coupling in diatomic molecules. Physical Review, 45, 98-103 (1934). Liens utiles Spectre de HCl Dans le site Hyperphysics, la page Vibration-Rotation Spectrum of HCl, en plus de constituer une mine d'or sur de nombreux concepts, définitions (utiliser l'index), présente aussi un spectre vibration rotation de HBr. Des explications théoriques et la description d'une expérience de laboratoire portant sur le spectre de HCl : Brucat, P. J. (1998). Physical Chemistry Laboratory - The Rotation / Vibration Spectrum of HCl, University of Florida Chemistry Dept., http://chem.ufl.edu/~itl/4411L_f00/hcl/hcl0.html [archive]. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||