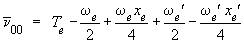|
|
|
|
MODULE 5 Sauts
électroniques dans les molécules diatomiques Préambule La molécule diatomique absorbe de l’énergie sous la forme de mouvements de rotation et de vibration. Elle peut aussi en absorber sous la forme de transition électronique. Cette absorption d’énergie est observable dans la région de l’ultraviolet. Quelles en sont les lois? Est-ce que les transitions de rotation et de vibration sont en même temps excitées? Est-ce que les lois qui régissent ces transitions sont conservées?
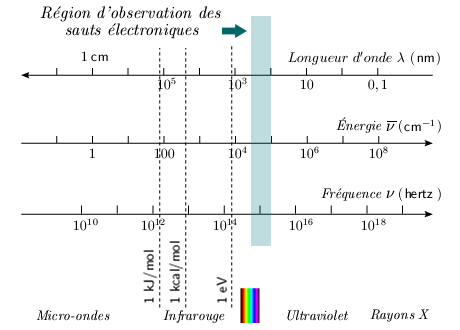
Faits expérimentaux On observe, dans la partie visible et ultraviolette du rayonnement électromagnétique (figure 5.1), des spectres d'émission et d'absorption. Ces spectres se présentent sous forme de bandes, sous faible dispersion. Ces bandes peuvent être résolues en raies sous dispersion élevée. Ces spectres sont en général très compliqués et nous n'entrerons pas dans le détail de leur structure.
On peut lier le nombre d'ondes correspondant à certaines têtes de bandes par la formule empirique :
Pour une seule molécule, on peut trouver plusieurs groupes de bandes qui peuvent être classées de cette façon. Les constantes b et c sont les mêmes que celles qui sont utilisées pour l'analyse des spectres de vibration (module 2 ). La structure de chaque bande peut également être analysée et les nombres d'ondes des raies reliés par une formule empirique :
Cette formule fait intervenir la constante a des spectres de rotation (module 1). Ces spectres se trouvent dans la région 0,5 μm à 0,1 μm et correspondent à des énergies de l'ordre de 240 à 1 200 kJ/mol, soit d'un ordre de grandeur bien supérieur aux énergies mises en jeu par la vibration ou la rotation. Comme c'est une énergie du même ordre que celle des sauts électroniques dans un atome, on admet que ces spectres sont l'indication d'un saut électronique dans la molécule coïncidant avec un changement dans les nombres quantiques de vibration et de rotation.
États électroniques d'une molécule En première approximation, une molécule peut être traitée à l'aide de la théorie simple de Bohr, c'est-à-dire que l'on peut admettre l'existence d'orbitales sur lesquelles seraient placés les électrons. À chaque orbitale correspondrait une énergie électronique bien définie. Les orbitales seraient discrètes, c'est-à-dire correspondraient à des valeurs discontinues de l'énergie. On peut aller plus loin et caractériser une orbitale par les nombres quantiques habituels : moment cinétique orbital l et moment cinétique de spin s. La somme géométrique de ces moments cinétiques caractérise l'état de la molécule. La notation sera parallèle à celle de l'atome en transposant les lettres capitales ordinaires en lettres capitales grecques.
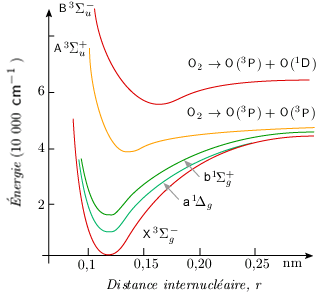
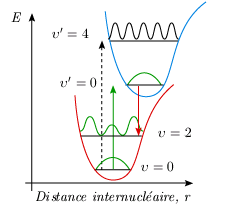
Chaque état correspond à une courbe de potentiel spécifique (figure 5.2) et à une valeur bien déterminée de l'énergie électronique, notée Te (figure 5.3), appelé terme électronique et exprimé en nombre d'ondes (unités : cm–1). On complète l'indication de l'état en notant le spin total en haut et à gauche, comme pour l'électron, par la valeur 2s + 1 (multiplicité). On aura ainsi des états 1Σ, 1Π pour un spin total nul, 2Σ, 2Π pour spin total 1/2, etc.
Normalement, il n'y a aucune raison pour que le nombre des états ne soit pas aussi grand que dans le cas de l'atome. En fait, on n'a observé pour chaque molécule étudiée (leur nombre en est encore très réduit) qu'un nombre restreint d'états électroniques : une quarantaine dans le cas de N2, O2 et NO; une vingtaine pour HCl et pour la plupart des autres molécules diatomiques. Ceci est lié au fait que nos connaissances dans ce domaine sont encore embryonnaires et proviennent de deux sources difficiles à exploiter : L'observation expérimentale des niveaux. Par suite de règles de sélection assez strictes, seules un petit nombre de transitions sont possibles; le nombre des spectres observables est donc assez limité. De gros efforts sont faits actuellement pour créer des conditions expérimentales spéciales qui rendent possibles les transitions interdites. La théorie. La théorie ne peut mener à des conclusions valables que pour des molécules très simples.
Diagramme des niveaux d'énergie et spectre observé Chacun des états électroniques ne correspond plus, comme dans le cas de l'atome, à des orbites plus ou moins éloignées du noyau. On peut dire que la configuration électronique est différente dans chaque cas, sans pouvoir en donner un schéma figuratif simple. Ce diagramme simplifié serait valable si la molécule n'était pas capable d'exécuter simultanément d'autres mouvements, c'est-à-dire si elle restait sans tourner à la distance internucléaire d'équilibre.
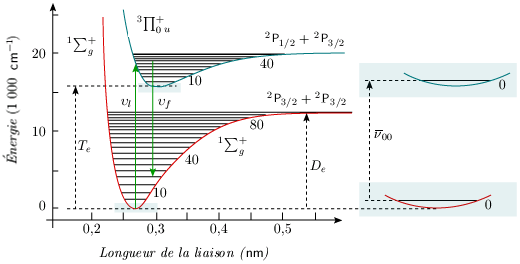
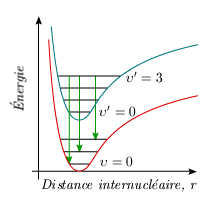
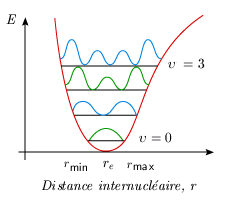
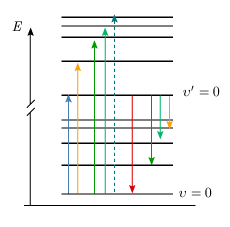
En fait, quel que soit l'état électronique considéré, la molécule vibre et tourne. Le modèle de l'oscillateur tournant (ou rotateur vibrant, voir (module 3) est valable pour chaque état électronique. À chaque état électronique correspond une courbe de potentiel avec les niveaux possibles d'énergie de vibration. Chaque courbe de potentiel est différente, avec sa propre valeur de la distance internucléaire, de l'énergie de dissociation, de la constante de force et de l'anharmonicité. De plus, sur chaque niveau de vibration viennent se superposer les niveaux possibles de rotation; la valeur de la constante de rotation est également différente dans chaque état électronique. C'est un peu comme si chaque état électronique correspondait à une nouvelle molécule. Le diagramme des niveaux d'énergie d'une molécule devrait donc se composer, pour chaque état électronique, d'un certain nombre de lignes horizontales, associées aux niveaux d'énergie de vibration et entre lesquelles on ferait figurer par des flèches les transitions possibles, soit en absorption, soit en émission. La figure 5.3 illustre ces niveaux pour l'état fondamental et un état excité de la molécule I2, tandis que l'animation associée à la même figure permet d'explorer, pour I2 et O2, le lien entre les mouvements de la molécule et divers états et niveaux de celle-ci.
Pour une molécule quelconque, et en ignorant l'énergie de translation, l'énergie totale est telle que : E = Etot = Eélec + Erot + Evib Ceci s'écrit, à l'aide des termes spectraux (unités : cm–1), de la façon suivante : E (cm–1) = Te + F(J) + G(υ) avec Eélec = hcTe. Il s'ensuit que l'énergie d'une molécule dans l'état électronique fondamental (Eélec = Te = 0) est donnée, en unités de nombres d'ondes, par :
et que celle d'une molécule dans un état électronique excité (Eélec = hcTe) est :
Les spectres observés dans le visible et l'ultraviolet résultent de transitions entre ces niveaux d'énergie de vibration et de rotation correspondant à deux états électroniques différents.
Spectre électronique - analyse rotationnelle Les transitions avec changement de niveau de rotation donnent une série de raies très rapprochées, prenant la forme d'une bande sous faible ou moyenne résolution. La structure de ces bandes s'analyse de la même façon que pour le spectre de rotation pure (module 1). La suite de raies de rotation (υ = υ') peut se mettre sous la forme d'un polynôme du 2e degré (en ignorant la distorsion due à la force centrifuge).
où a = B + B′, c = B – B′ et b une constante qui dépend du niveau de vibration et de l'état électronique excité en cause. Comparativement au spectre de rotation-vibration normal (sans saut électronique), le problème se complique du seul fait que les valeurs de B et de B′ sont en général très différentes puisque les distances internucléaires sont généralement très affectées (beaucoup plus que dans les changements de niveaux de vibration). Il découle de cette observation que la portion de parabole observée (la parabole de Fortrat) se situe au voisinage de son sommet. Dans le spectre de rotation-vibration, la suite de raies apparaît sous une forme continue : l'énergie E est une fonction croissante de m, avec une légère courbure vers le bas (voir, dans le module 3, la figure 3.6); dans ces conditions, il est facile d'indexer les raies. Dans le cas présent, la valeur du paramètre c beaucoup plus grande entraîne une courbure prononcée, de sorte que l'énergie E est croissante avec m dans une portion de la parabole et décroissante avec des valeurs croissantes de m pour une autre portion. Cela a pour effet de faire se voisiner, dans le spectre, des raies associées à des valeurs de m différant de plusieurs unités. Afin d'indexer les raies convenablement, on doit utiliser une méthode appropriée, comme celle de la deuxième différence (voir module 1).
Spectre électronique - analyse vibrationnelle Dans la section précédente on a envisagé le cas où la transition électronique ne mettait pas en jeu de transition vibrationnelle : Δυ = 0. On dit alors que la transition observée correspond à la bande 0-0. Dans ce cas, l'énergie
nécessaire est l'énergie requise pour passer
de l'état 1 (niveau υ = 0)
à l'état 2 (niveau υ' = 0),
notée Comme la règle de sélection Δυ = 0, ±1, ±2, ±3, ... est plutôt large et que les énergies disponibles sont plutôt importantes, on observe non pas seulement la bande 0-0, mais toute une variété de bandes correspondant aux transitions possibles entre les divers niveaux de vibration. Ainsi, l'énergie des bandes dont le
niveau d'origine est υ = 0,
notée On retrouve dans ce cas particulier l'origine de la formule 5.1, qui décrit l'absorption à partir du niveau υ = 0 d'un état électronique vers les divers niveaux de vibration d'un autre état électronique, donnant une série de bandes presque régulièrement espacées, d'énergie : Ceci peut aussi s'écrire :
En fonction des mêmes
paramètres, l'énergie de la transition
électronique pure (υ = υ' = 0),
notée
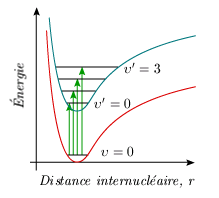
En spectroscopie d'absorption, l'état fondamental de vibration, υ = 0, est souvent le seul peuplé; il s'ensuit que les bandes électroniques s'organisent dans une suite, une progression, qui suit la valeur de υ' (figure 5.4).
Le tableau 5.1 systématise les énergies des transitions en absorption de même que les premières et secondes différences entre les énergies de ces raies. Tableau 5.1.
Transitions vibrationnelles en absorption
Par contre, en émission, puisque de nombreux états de vibration sont excités, le nombre de bandes devient beaucoup plus grand, et les séries sont plus nombreuses. En fait on doit s'attendre à autant de séries qu'il y a de niveaux de vibration à émettre. Le tableau 5.2 donne un exemple de séries de bandes observées. Tableau 5.2.
Transitions vibrationnelles observées dans
N2
En ne retenant que les bandes qui partent du même niveau de vibration υ' et ayant n'importe quelle valeur υ pour niveau final (figure 5.5), l'énergie des transitions peut se mettre sous la forme :
ce qui peut s'écrire plus simplement :
où a, qui regroupe tous les termes en υ', est une constante, la seule variable étant υ (υ' est fixe).
Le tableau 5.3 systématise les énergies des transitions en émission de même que les premières et secondes différences entre les énergies de ces raies. Tableau 5.3. Transitions vibrationnelles en émission.
Remarque La valeur de a du tableau précédent est telle que : a = Il s'ensuit que a dépend de υ' et il y a donc autant de séries de bandes qu'il y a de niveaux υ' d'où proviennent les transitions.
Détermination des constantes moléculaires Puisque les constantes moléculaires peuvent être déterminées à partir des spectres de vibration-rotation, on peut se demander ce que nous apporte de plus la spectroscopie électronique des molécules. Voici quelques éléments de réponse.
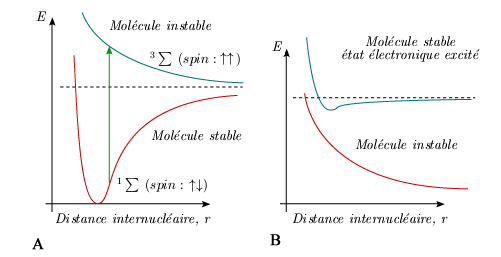
Courbes de potentiel correspondant à des états instables La formation d'une molécule à partir de deux atomes, dans un état quelconque, ne conduit pas toujours à une courbe de potentiel à minimum. Dans ce cas, la molécule formée est instable et les atomes se séparent au bout d'un temps plus ou moins long, mais non négligeable (voir le cas de l'hydrogène, figure 5.6A). Notons que si l’état fondamental est stable comme dans le cas de l’hydrogène moléculaire, il peut en être autrement dans d’autres cas. Ainsi l'état fondamental des molécules de gaz rare, tel Xe2 ou He2, est instable. La molécule existe cependant de manière stable dans certains états électroniques excités (figure 5.6B).
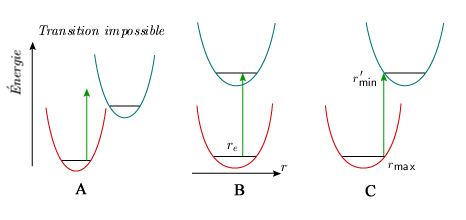
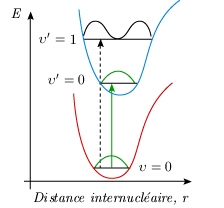
Le principe de Franck-Condon Le passage d'une molécule d'un état électronique à un autre est très rapide. Considérons le passage d'un photon à travers le nuage électronique d'une molécule. Ce nuage voit passer une perturbation à laquelle est associée un vecteur champ électrique orienté perpendiculairement à la direction de propagation. En supposant que le nuage a un diamètre de 0,3 nm, la perturbation électromagnétique le traverse en : d = υt ⇒ t = 0,3 10–9 m / 3 108 m/s = 10–18 seconde. On admet que la transition, le saut électronique, s'opère dans un temps très court de l'ordre de 10–15 – 10–17 seconde. Considérons maintenant une vibration moléculaire. Ce mouvement intramoléculaire du réseau nucléaire est beaucoup plus lent. En réalité, les vibrations les plus rapides s'effectuent en quelque 10–13 s. Il s'ensuit que la géométrie de la molécule demeure inchangée pendant un saut électronique. Cette remarque est également valable en ce qui regarde les mouvements de rotation. On peut donc conclure que la géométrie de la molécule est inchangée pendant un saut électronique. Du point de vue de la mécanique quantique, cela se traduit par le fait que pour qu'un saut électronique se produise, les fonctions d'onde associées aux deux états doivent se chevaucher. On interprète cette condition en termes classiques en disant que la distance internucléaire ne doit pas changer lors du saut électronique. C'est le principe de Franck-Condon. Sur un graphique où l'on représente les courbes de potentiel et les niveaux de vibration-rotation des deux états, une transition entre deux niveaux sera impossible si on ne peut relier ceux-ci par une ligne verticale (figure 5.7A). De même, la présence d'une gamme plus large de longueurs de liaison communes aux deux états sera associée à une plus grande probabilité de transition. Ainsi les configurations B et C de cette dernière figure sont beaucoup plus favorables à la transition que la configuration A.
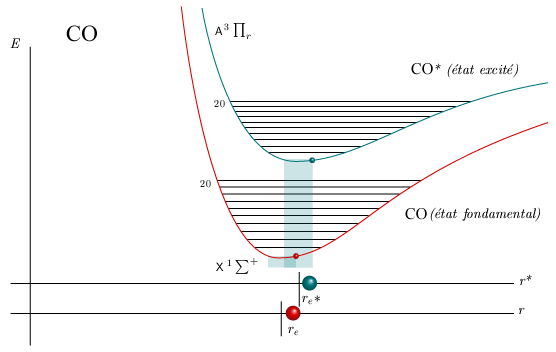
L'animation de la figure 5.8 permet de visualiser, pour l'état fondamental et deux états excités des molécules de CO et H2, cette gamme de longueurs de liaison communes pour divers niveaux de vibration. La largeur des rectangles translucides correspond à la gamme des longueurs de liaison pour chacun des deux niveaux; la largeur de leur intersection fournit une idée approximative de la probabilité de la transition.
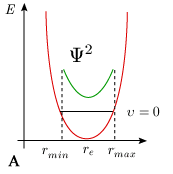
Ajoutons que le temps de séjour de la molécule avec une distance internucléaire comprise entre r' et r' + dr' n'a pas la même valeur entre chaque point de la trajectoire situé entre rmin et rmax. Le modèle mécanique de l'oscillateur prévoit que la molécule passe la majorité de son temps au voisinage des extremums, là où la vitesse dx / dt est minimum, c'est-à-dire aux abscisses rmin et rmax. Au contraire, sa durée de séjour au voisinage de re est minimum puisque la valeur dx / dt est maximum (figure 5.9A).
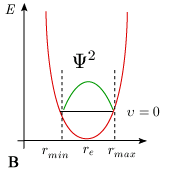
La mécanique quantique prévoit exactement le contraire. La solution de l'équation de Schrödinger pour l'oscillateur (harmonique ou anharmonique) conduit à une fonction d'onde dont le carré (la probabilité de présence d'une distance internucléaire donnée) est maximal pour r = re et minimal aux extremums, à tout le moins pour le niveau de vibration υ = 0 (figure 5.9B). Cette description correspond beaucoup mieux à la réalité physique que celle fournie par la mécanique classique. La situation est un peu plus complexe sur les niveaux supérieurs de vibration. Pour un niveau υ > 0, le carré de la fonction d'onde admet υ + 1 maxima et l'on peut montrer que les extremums les plus importants sont situés près des extrémités du segment vibrationnel (figure 5.10). Pour les nombres quantiques élevés, la distribution de probabilité de présence se rapproche donc à certains égards de la valeur classique.
Quoi qu'il en soit, compte tenu du fait que la probabilité de trouver la distance internucléaire à l'intérieur d'un élément dr' varie considérablement avec l'abscisse r', la probabilité de transition, donc l'intensité de la transition (de la bande) observée, sera très affectée par la distribution de probabilité de la distance internuclaire entre rmin et rmax.
La fluorescence Considérons l'absorption d'énergie entre l'état fondamental et un état électronique excité. Supposons aussi que ces deux états électroniques se déduisent l'un de l'autre par translation selon un axe parallèle à l'axe énergie. Les deux courbes de potentiel admettent donc la même valeur de r à l'équilibre, re = re' (figure 5.11).
En absorption et aux températures usuelles, toutes les molécules se trouvent dans l'état électronique fondamental et dans le niveau υ = 0. La transition se fera principalement à partir de l'abscisse re puisque c'est dans cette configuration que la molécule a le plus de chance de se trouver. Le principe de Franck-Condon établit que la transition électronique est beaucoup plus rapide qu'un mouvement de vibration, de telle sorte que la distance internucléaire r demeure inchangée au cours de la transition. La molécule décrit donc sur le graphe (figure 5.11) un chemin «vertical» sans variation de valeur de r. La probabilité de passage entre υ = 0 et un niveau υ', entre l'abscisse r et r + dr, dépend du produit des probabilités de trouver la distance internucléaire possédant cette valeur sur chacun des deux états électroniques. La probabilité de la transition est égale à ce produit, intégré entre les valeurs rmin et rmax. On réalise alors que la transition υ' → υ (0 → 0) est très probable (raie intense). Les transitions (υ' → 0) ne sont pas interdites; elles sont moins probables et les intensités des bandes correspondantes décroissent avec l'accroissement de υ'. Les niveaux υ' sont peuplés par absorption d'énergie (flèches vers le haut dans la partie gauche de la figure 5.12). Les molécules ainsi excitées redescendent très rapidement par conversion interne vers le niveau fondamental de cet état électronique excité, soit vers le niveau υ' = 0. Certaines molécules, pour revenir
à l'état électronique fondamental,
n'ont alors d'autre choix que de fluorescer : elles
réémettent un photon en revenant vers
l'état fondamental. L'émission a lieu au cours
du passage entre le niveau υ' = 0
et l'un des niveaux υ. Par le
même raisonnement, on montre que la transition υ' → υ
(0 → 0) est la plus probable (la plus
intense) (flèche rouge vers le bas dans la
figure 5.12). Il est d'ailleurs intéressant de
comparer le spectre d'absorption et le spectre
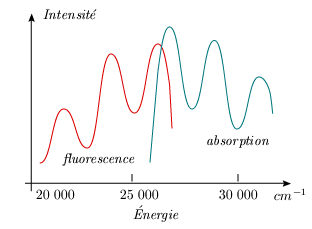
d'émission. Le spectre de la fluorescence
apparaît comme l'image miroir du spectre d'absorption
(figure 5.13). Le décalage entre le maximum de
chaque courbe, qui correspond à la transition
vibrationnelle
Dans le cas de la molécule d’oxygène, la transition entre le premier état électronique excité 1Δg et l’état fondamental 3Σg– est interdite puisqu’elle exige un changement de parité électronique, la molécule passant d’un état singulet (tous les électrons sont associés par spin antiparallèle) vers un état triplet (deux électrons non appariés ont leur spin parallèle). En haute atmosphère, au-dessus de 50 km d’altitude, l’ozone est décomposé par le rayonnement ultraviolet très lointain (λ < 307,5 nm). Il se forme des molécules d’oxygène sup>1Δg. Ces molécules n’ont pas la possibilité de perdre leur énergie électronique par transfert vers une autre molécule. Les pressions et les concentrations de molécules y sont très basses. De plus, lorsque les collisions existent, l’efficacité du transfert d’énergie y est très faible. Il s’ensuit que la seule possibilité de retour vers l’état fondamental réside dans la phosphorescence. Le temps de vie de la molécule électroniquement excitée est de l’ordre de 1 heure. Cette transition est facilement observable pourvu que l’observateur se trouve dans cette région de l’espace où la lumière émise n’est pas absorbée par d’autres molécules. On observe une émission dans la région de l’infrarouge vers 1270 nm. Le maximum de cette émission correspond à la transition entre les niveaux de vibration υ = 0 de chacun des deux états électroniques, car la distance internucléaire moyenne pour chacun des deux niveaux est semblable : re (3Σg–) = 1,2075 nm et re (1Δg) = 1,2156 nm (voir figure 5.2). Ce cas de figure correspond à la situation décrite à la figure 5.11. Supposons au contraire que les courbes de potentiel ne se déduisent plus l'une de l'autre selon une translation verticale, mais plutôt oblique, de telle sorte que re' = re ou mieux re' > re (figure 5.14). La figure montre que la transition υ' → υ (4 → 0) est la plus probable. Une fois peuplé, ce niveau υ' = 4 se dépeuple au profit des niveaux υ' inférieurs et finalement au profit du seul niveau υ' = 0. En émission, c'est au tour de la transition υ' → υ (0 → 2) d'être favorisée. Ceci bien sûr n'exclut pas complètement les transitions 0 → 3, 0 → 4, ...
De nouveau le cas de l’oxygène est intéressant. On a pu observer l’absorption entre l’état fondamental et l’état électronique excité triplet 3Σu– (bande Schumann-Runge) de même que la fluorescence entre ces deux états. Cette fois les distances interatomiques sont très différentes : r (3Σg–) = 1,2075 nm et r (3Σu–) = 1,6042 nm (voir figure 5.2). Ce cas d’espèce correspond à la figure 5.14.
Effet isotopique Les états électroniques ne sont pas affectés par la substitution isotopique puisque les énergies des couches électroniques ne dépendent pas de la masse du noyau mais seulement de sa charge.
Conclusions Les transitions électroniques exigent une quantité d’énergie de beaucoup supérieure à celle qui est requise pour exciter les mouvements internes d’une molécule. Ces transitions sont également soumises à leurs propres lois. Lors d'une transition électronique, les transitions de rotation et de vibration sont donc simultanément excitées. Les règles de sélection et les lois s'appliquant à celles-ci sont conservées. Avec un appareil de haute dispersion, on saura donc voir les transitions de vibration-rotation au sein d’un spectre d’absorption électronique. Ces possibilités existent tant en absorption qu’en émission (fluorescence).
Pour en savoir plus Liens utiles Le spectre de fluorescence de l'iode : http://itl.chem.ufl.edu/4411L_f96/i2_lif/i2_lif_il.html [archive]. Ce site du professeur P. J. Brucat présente plusieurs aspects reliés au traitement de la molécule d'iode. On y trouve des éléments reliés à la courbe de potentiel, au traitement de l'équation de Schrödinger, à l'appareillage expérimental, au traitement des données, à l'application de la méthode de Birge-Spooner, etc. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

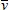 = d + bk – ck2
k = nombre
entier
= d + bk – ck2
k = nombre
entier