|
|
|
|
MODULE 4 Diffusion de
la lumière - effet Raman Préambule La diffusion de la lumière par une molécule diatomique obéit à des lois bien précises. On distingue plusieurs processus de diffusion. Parmi ceux-ci, on retrouve l’effet Raman qui met en cause des transitions entre divers niveaux d’énergie de rotation et de vibration. Quelles sont les lois qui décrivent l'effet Raman? Quel est l’intérêt de cet effet pour la connaissance des molécules?
Introduction L'effet Raman résulte d'un processus de diffusion de la lumière par les molécules. Nous commencerons donc par étudier le phénomène de diffusion normale avant de passer à l'effet Raman. Notons dès maintenant que le processus de diffusion de la lumière par des molécules se distingue aussi des phénomènes étudiés en spectroscopie micro-onde (module 1) et en spectroscopie infrarouge (module 2). Dans ces derniers phénomènes, il y avait soit absorption, soit émission de lumière. À l'échelle de la molécule on dira qu'il y avait soit absorption, soit émission de photon. Dans le cas de la diffusion, comme le laisse supposer le mot, la lumière est déviée de sa trajectoire au moment où elle passe dans le champ moléculaire. Sans entrer davantage dans les détails de ce mécanisme d'interaction molécule-photon, la diffusion est le résultat d'une interaction de nature différente de celle observée et étudiée en spectroscopie.
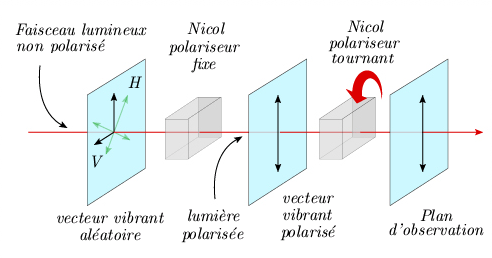
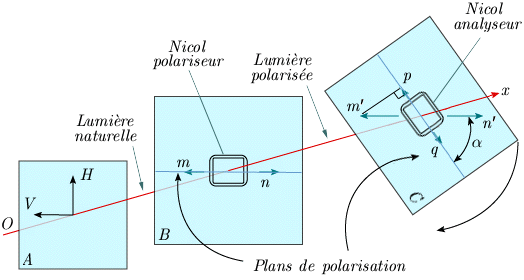
Diffusion de la lumière Nous étudierons d'abord la diffusion de la lumière par un milieu trouble (un milieu transparent contenant des particules), ce que l'on nomme l'effet Tyndall. Nous verrons ensuite le même phénomène lorsque ces particules sont des molécules et finalement nous considérerons la propriété de polarisation de la lumière.
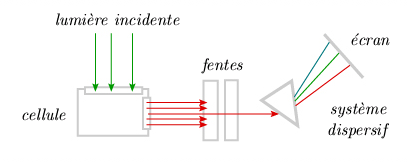
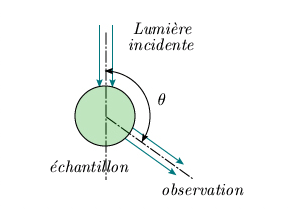
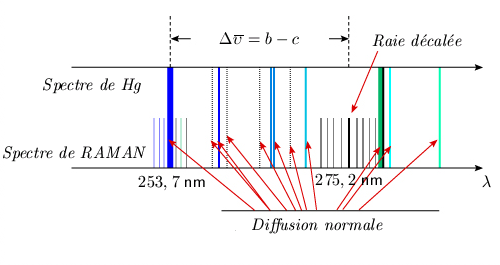
Effet Raman - observation expérimentale Ce phénomène a été prédit par Adolf Smekal en 1923, et décrit théoriquement par les fondateurs de la mécanique quantique (Heisenberg en 1925, Schrödinger en 1926, Dirac en 1927). Il a été observé expérimentalement par le savant indien Sir Venkata Raman en 1928. Deux chercheurs russes, Grigori Landsberg et Leonid Mandelstam, ont aussi observé indépendamment et presque simultanément cet effet. Malencontreusement, l'Histoire n'a pas retenu le nom de ces derniers. Cet effet, au contraire de la diffusion normale, fait intervenir les propriétés internes de la molécule. Examinons de plus près les phénomènes observables. On éclaire latéralement, au moyen d'une raie monochromatique très intense, une substance (diatomique ou polyatomique, mais nous ne traiterons ici que le cas de la molécule diatomique). On analyse au spectrographe la lumière diffusée perpendiculairement à la direction d'éclairement. En général, on utilise l'une ou l'autre des raies intenses visibles et ultraviolettes émises par l'arc au mercure (253,7 nm, 404,7 nm ou 435,8 nm), isolées au moyen d'un filtre approprié. On utilise aussi de plus en plus des raies émises par des lasers éclairant dans le visible, qui émettent une radiation beaucoup plus monochromatique (par exemple un laser à argon émettant à 514,5 nm). Dans la lumière analysée, on trouve une raie dont la longueur d'onde est la même que celle de la radiation incidente. Cette raie est due à la diffusion normale dont il a été question plus haut. En plus de cette raie, on en observe une autre, beaucoup moins intense, décalée vers les grandes longueurs d'onde (figure 4.5). Si la raie excitatrice est très intense, et si on prend beaucoup de précautions pour diminuer l'intensité de la raie due à la diffusion normale, on observe de part et d'autre de celle-ci une série de raies très faibles approximativement équidistantes.
Dans le cas de HCl, l'intervalle de
fréquence Δ 2a = 2 × 20,60 = 41,20 cm-1 Ces nombres sont si voisins des nombres tirés de l'effet Raman que l'on peut dire dès maintenant que la raie éloignée est certainement liée à la vibration de la molécule, les autres raies étant liées à la rotation. Nous sommes donc en présence d'un effet de diffusion de la lumière dans lequel il y a interaction entre la lumière incidente et la molécule. Puisqu'il y a variation de fréquence de la lumière diffusée, il y a échange d'énergie entre la radiation électromagnétique et la molécule. Au contraire, la diffusion normale se fait sans échange d'énergie. On peut comparer ces deux phénomènes à une collision élastique et à une collision inélastique entre une masse en mouvement et une autre, beaucoup plus grande et immobile. Dans la collision élastique, l'énergie cinétique totale, égale à l'énergie de la masse en mouvement, est conservée. La masse en mouvement repart avec la même énergie cinétique qu'avant la collision; l'énergie cinétique acquise par la masse immobile est négligeable. Dans la collision inélastique, par contre, l'énergie cinétique totale change lors de la collision; l'énergie perdue ou acquise par la masse en mouvement est associée à une augmentation ou une diminution d'une même quantité d'énergie, mais sous une autre forme, par exemple l'énergie potentielle (interne) de la masse immobile. Nous verrons qu'il en est de même dans le cas de l'effet Raman.
Théorie de l'effet Raman Considérons une onde
électromagnétique incidente de
fréquence ν, donc d'énergie
hc
Comme Δ Si la molécule passe du niveau de vibration υ = 0 au niveau υ = 1, l'énergie qu'il lui faut est :
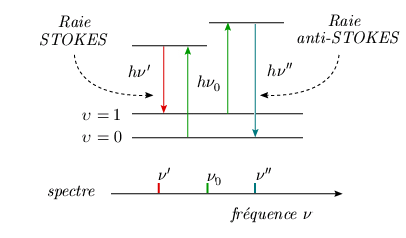
Cas de HCl : Δ On retrouve la valeur du déplacement de la raie éloignée. Cette raie est donc bien due à un échange d'énergie avec transition de vibration. D'autre part, il y a diminution d'énergie de la radiation initiale, donc diminution de la fréquence, ce qui entraîne un déplacement vers les grandes longueurs d'onde. Une règle de sélection Δυ = ±1 interdit pratiquement les sauts à des niveaux plus élevés que 1 à partir du niveau fondamental. On peut se demander pourquoi on ne pourrait observer le processus inverse, soit une cession d'énergie de la molécule dans l'état υ = 1 avec passage de cette dernière à l'état υ = 0. On devrait dans ce cas observer une raie vers les courtes longueurs d'onde, symétrique de la première. Cette raie n'est pas observable parce que la population du niveau υ = 1 est très faible à la température ordinaire. En effet, on peut montrer qu'à la température normale, le nombre de molécules diatomiques qui se trouvent avec une énergie correspondant au niveau de vibration υ = 1 est, de plusieurs ordres de grandeurs, plus petit que le nombre de molécules situées sur le niveau υ = 0. Pour trouver une population significative du niveau υ = 1, il faut que l'énergie nécessaire pour atteindre ce niveau soit comparable à l'énergie disponible à la température de la molécule. On retrouve ce type de conditions, par exemple, dans des molécules diatomiques de masse réduite élevée, tel l'iode I2, ainsi que dans certaines molécules plus complexes. Dans ces cas les deux raies sont observées, la raie décalée vers les petites longueurs d'onde (ou les énergies élevées), appelée raie anti-Stokes, étant toujours moins intense que la première, la raie Stokes (Figure 4.6).
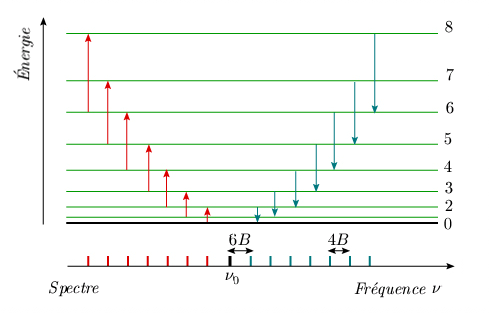
De son côté, le spectre de raies équidistantes (figure 4.7) est dû à des transitions avec échange d'énergie entre les niveaux de rotation. Comme plusieurs de ces niveaux sont peuplés à la température ordinaire, on observe des raies de chaque côté de la raie excitatrice.
L'intervalle des raies est le double de l'intervalle observé dans le spectre infrarouge car la règle de sélection est différente :
En ignorant l'effet de la distorsion centrifuge ou encore en posant D = 0, l'énergie d'une raie quelconque est :
De la même manière, la différence d'énergie entre les niveaux J + 3 et J + 1 est : Δ(J + 3,
J + 1) =
B (J + 3)(J + 4)
-
B (J + 1)(J + 2) de telle sorte que la différence entre deux raies successives est :
Cette relation permet d'obtenir la valeur de la constante de rotation B et donc de calculer les distances internucléaires (voir le tableau 1.2 du module 1). Avec un appareil de grande dispersion, on obtient de la même manière que pour les molécules hétéronucléaires les constantes de distorsion centrifuge D (tableau 4.1). Tableau 4.1. Quelques caractéristiques physiques de molécules diatomiques homonucléaires.
Ce tableau confirme bien qu'en général la constante de distorsion centrifuge est négligeable devant la constante de rotation B.
Condition nécessaire à l'obtention de raies Raman - polarisabilité d'une molécule La variation de moment dipolaire de la molécule est une condition nécessaire pour qu'un saut puisse se faire entre deux niveaux par absorption ou émission spontanée, que ce soit en rotation (module 1) ou en vibration (module 2). Mais dans le cas de l'effet Raman, ce qui est requis est une variation non pas du moment dipolaire, mais plutôt de la polarisabilité de la molécule. Si on soumet une molécule à un champ électrique, on va assister à une déformation du nuage électronique due à l'action du champ; une radiation électromagnétique possède un champ électrique et produit donc cet effet. Cette déformation entraîne l'apparition d'un moment dipolaire induit; ce dernier est proportionnel à la polarisibilité de la molécule. Or, le nuage électronique n'a pas exactement la même forme pour différents niveaux de vibration. On peut imaginer que sa tendance à se déformer sera également différente. C'est le phénomène qui constitue une variation de polarisabilité de la molécule. En raison de leur symétrie, les molécules diatomiques homonucléaires ont un moment dipolaire permanent nul. Cependant, leur polarisabilité varie avec le niveau d'énergie de vibration. Bien qu'elles n'absorbent pas dans l'infrarouge, ces molécules présentent donc un spectre Raman, tout comme les molécules diatomiques hétéronucluaires.
Spectre Raman et spectre d'absorption infrarouge On pourrait croire qu'on obtient les mêmes informations à l'aide des bandes d'absorption de vibration pure et des raies Raman de vibration. C'est partiellement vrai pour les molécules polyatomiques (voir module 6). Pratiquement, le spectre de rotation Raman étant très difficile à observer, il est peu utilisé et le spectre de rotation pure ou de rotation-vibration reste la meilleure source d'informations. L'effet Raman constitue cependant un complément non négligeable dans l'étude des structures puisque certaines transitions ne sont pas actives en absorption infrarouge (molécules diatomiques homonucléaires, par exemple) et qu'elles le sont en Raman. L'inverse est aussi vrai : certaines transitions actives en spectroscopie infrarouge ne le sont pas en Raman. La détermination des fréquences de vibration peut se faire par l'une ou l'autre des deux méthodes, complémentaires, la spectroscopie Raman présentant certains avantages et inconvénients par rapport à la spectroscopie infrarouge. Avantages du spectre Raman
Inconvénients du spectre Raman
Conclusions L'effet Raman, un processus de diffusion de la lumière par les molécules, obéit à des exigences et donc à des lois différentes de celles qui s'appliquent à l'absorption et à l'émission. C’est la variation de polarisabilité de la molécule qui gouverne ce processus. Les règles de sélection sont modifiées et l’on a accès dans certains cas à des informations non disponibles en spectroscopie infrarouge.
Pour en savoir plus Liens utiles Une série de biographies, dont celle de Sir C. V. Raman : http://biography-of.com/c-v-raman. Un court texte qui décrit de
manière simple l'effet Tyndall : Gibbs, P.,
Why is the sky blue? Un site général en physique qui
contient beaucoup d'information sur de nombreux
phénomènes physiques. On trouvera en
particulier à l'adresse indiquée des
présentations sur la diffusion Rayleigh, ou
«Pourquoi le ciel est bleu?» |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

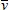 .
L'onde peut céder une partie de cette énergie
à la molécule; cette partie
cédée peut être employée à
faire passer la molécule de son niveau fondamental
vers l'un des ses niveaux excités. Si hc Δ
.
L'onde peut céder une partie de cette énergie
à la molécule; cette partie
cédée peut être employée à
faire passer la molécule de son niveau fondamental
vers l'un des ses niveaux excités. Si hc Δ