|
|
MODULE 5 Sauts électroniques dans les molécules diatomiques
Problèmes
-
Les valeurs de ωe
et ωexe
pour 12C16O dans l'état électronique fondamental
sont respectivement 2 170,2 et 13,5 cm–1.
On observe un spectre électronique et l'on croit pouvoir identifier
les têtes de bandes telles qu'indiquées dans le tableau suivant :
|
υ' ←
υ
|
Énergie
(cm–1)
|
| 1 ←
0 |
66 227 |
2 ←
1 |
65 532 |
3 ←
2 |
64 829 |
4 ←
3 |
64 118 |
5 ←
4 |
63 399 |
Note : le signe '
(prime) est réservé pour l'état électronique excité.
- Calculez ωe'
et ωe' xe'.
- Calculez l'énergie
 00
de la transition électronique pure. 00
de la transition électronique pure.
- Calculez, pour l'état fondamental et pour l'état excité, l'énergie
de dissociation spectroscopique.
- Calculez l'énergie de dissociation chimique de chaque état électronique.
Corrigé
-
-
Une transition électronique du
radical SiCl2 a été étudiée en émission vers 330 nm
(Sameith, D. et autres, Chem. Phys. Lett., 128,
483, 1986). On rapporte les données expérimentales dans le tableau
ci-joint (Schème de Deslandres).
Tableau de Deslandres de
la bande de SiCl2 située vers 330 nm.
υ
υ'
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
0 |
30 311 |
30 113 |
29 911 |
29 713 |
29 519 |
29 318 |
29 122 |
28 917 |
1 |
30 456 |
30 261 |
30 063 |
29 862 |
29 668 |
|
29 267 |
29 070 |
2 |
30 606 |
30 411 |
30 212 |
30 009 |
|
29 622 |
29 419 |
29 217 |
3 |
30 757 |
30 558 |
30 361 |
30 159 |
29 960 |
29 761 |
29 568 |
29 371 |
4 |
30 910 |
30 708 |
30 509 |
|
|
|
|
|
5 |
31 061 |
30 857 |
|
|
|
|
|
|
6 |
31 211 |
31 008 |
30 804 |
|
|
|
|
|
7 |
31 362 |
|
30 953 |
|
|
|
|
|
| 8 |
31 509 |
|
|
|
|
|
|
|
Par un moyen électronique approprié,
déterminez les valeurs de ωe
et ωexe
pour chacune des séries de bandes suivantes :
-
dans la série υ'
→ υ (x
→ 0)
-
dans la série υ'
→ υ (x
→ 1)
-
dans la série υ'
→ υ (x
→ 2)
Corrigé
-
Faites le même exercice avec les
séries de bandes suivantes :
-
dans la série υ'→
υ (0 →
y)
-
dans la série υ'→
υ (1 →
y)
-
dans la série υ'→
υ (2 →
y)
-
dans la série υ'→
υ (3 →
y)
Corrigé
-
Déduisez-en l'énergie électronique
de la transition électronique pure, en utilisant au moins sept
(7) valeurs calculées de manière indépendante. Corrigé
-
La bande fondamentale ν1
de CO est située à 2 143,3 cm–1 et la première
harmonique 2ν1, est
située à 4 259 cm–1.
a. Calculez ωe,
ωexe,
la constante de force de la liaison et le nombre de vibrations par
seconde de la molécule. Évaluez en cmcm–1 l'énergie de
dissociation de la molécule.
b. On observe les transitions combinées
(électroniques et vibration) suivantes :
|
υ'←
υ
|
Énergie (cmcm–1)
|
|
5' ← 4
|
63 399
|
|
4' ← 3
|
64 118
|
|
3' ← 2
|
64 829
|
|
2' ← 1
|
65 532
|
|
1' ← 0
|
66 229
|
En utilisant la méthode de la première,
puis de la deuxième différence, déterminez la valeur de ωe' xe'
du niveau excité électroniquement. Déterminez également
l'énergie en cmcm–1 de la transition électronique pure.
c. Calculez les points d'énergie zéro
pour l'état fondamental et pour l'état électronique excité. En déduire
l'énergie de la transition électronique pure et l'énergie de
dissociation de l'état électronique excité (en cmcm–1 et
en joules).
d. Tracez à l'échelle les courbes
de Morse de l'état fondamental et de l'état électronique excité,
en y portant dans chaque cas les quatre premiers niveaux de vibration.
Note : il n'y a pas de corrigé
pour ce problème et le suivant.
-
Analysez les données obtenues pour
les têtes de bandes suivantes (υ
= état fondamental, υ'
= état électronique excité) : en prenant deux séries appropriées
de bandes, déterminez ωe,
ωexe,
ωe'
et ωe' xe'
(énergie en cm–1).
|
υ
υ'
|
0
|
1
|
2
|
3
|
| 0 |
29 647,5 |
28 167,5 |
26 707,5 |
25 267,5 |
1 |
30 407,5 |
28 927,5 |
27 467,5 |
26 027,5 |
2 |
31 127,5 |
29 647,5 |
28 187,5 |
26 747,5 |
3 |
31 807,5 |
30 327,5 |
28 867,5 |
27 427,5 |
4 |
32 447,5 |
30 967,5 |
29 507,5 |
|
5 |
|
31 567,5 |
30 107,5 |
28 667,5 |
6 |
|
|
30 667,5 |
29 227,5 |
-
Étude de l'oxygène : Slanger,
T. G. et P. C. Cosby. J. Phys. Chem., 92, 267 (1988).
-
On mesure les constantes rotationnelles
de la molécule O2 dans le niveau de vibration fondamental
(υ = 0) des six
premiers états électroniques :
| État
électronique |
B (υ = 0)
(cm–1) |
X 3Σg– |
1,437 67 |
a 1Δg |
1,417 801 |
b 1Σg+ |
1,391 26 |
c 1Σu– |
0,910 69 |
A' 3Δu |
0,903 40 |
A 3Σu+ |
0,904 52 |
Calculez la distance internucléaire
dans chacun de ces états électroniques.
-
La molécule O2 présente les niveaux
énergétiques G (υ)
(cm–1) apparaissant dans le tableau suivant :
|
États électroniques
|
υ = 0
|
υ = 1
|
υ = 2
|
υ = 3
|
υ = 4
|
X 3Σg– |
0 |
1 556,4 |
3 089,2 |
|
|
| a 1Δg |
7 889,4 |
9 373,1 |
10 830,6 |
|
|
b 1Σg+ |
|
14 527,0 |
15 903,8 |
|
|
c 1Σu– |
|
33 434,0 |
34 174,8 |
34 886,1 |
|
A' 3Δu |
|
|
35 933,1 |
36 661,0 |
37 354,8 |
A 3Σu+ |
35 010,2 |
35 784,6 |
36 528,6 |
|
|
Calculez, pour chacun des états électroniques,
ωe,
ωexe,
De
et l'énergie zéro G(0).
Corrigé.
-
Une analyse plus poussée de l'état b 1Σg+
permet d'obtenir les valeurs G(υ),
en cm–1, suivantes :
|
υ
|
G(υ)
|
υ
|
G(υ)
|
0 |
13 122,24 |
4 |
18 573,20 |
1 |
14 527,00 |
5 |
19 865,91 |
2 |
15 903,75 |
6 |
21 130,61 |
3 |
17 252,48 |
7 |
22 367,30 |
En utilisant la méthode des différences calculez
les valeurs ωe,
ωexe,
De
et G(0)
pour cet état excité.
-
De la même manière, on obtient pour l'état (X 3Σg–) :
|
υ
|
G(υ)
|
υ
|
G(υ)
|
υ
|
G(υ)
|
0 |
0 |
5 |
7 548,27 |
10 |
14 523,53 |
1 |
1 556,387 |
6 |
8 988,73 |
11 |
15 850,60 |
2 |
3 089,19 |
7 |
10 406,42 |
12 |
17 154,96 |
3 |
4 598,65 |
8 |
11 801,46 |
13 |
18 436,53 |
4 |
6 084,96 |
9 |
13 173,80 |
14 |
19 695,20 |
En utilisant un moyen électronique
approprié, effectuez les régressions d'ordre 2, 3, 4 et 5. Dans
chaque cas indiquez les valeurs ωe,
ωexe,
De
et G(0).
Expliquez pourquoi, à partir des équations E = f (υ)
obtenues, on trouve que l'ordonnée à l'origine s'approche de plus
en plus de zéro avec l'augmentation de l'ordre.
Problèmes avec VR Molécules
-
Placez VR Molécules à la page
3. En faisant varier si nécessaire les nombres quantiques, déterminez
les valeurs des constantes re,
Te,
ωe,
ωexe
et Be pour
les deux états de la molécule d'iode, soit I2 (état fondamental
X 1Σg+)
et I2* (état excité B 3Π0+u).
Déterminez aussi l'énergie de la transition  00
entre les deux états. Note : ne pas oublier d'activer la correction
pour l'anharmonicité. Corrigé 00
entre les deux états. Note : ne pas oublier d'activer la correction
pour l'anharmonicité. Corrigé
-
La page
4 et la page 5
de VR Molécules permettent de comparer la molécule d'hydrogène dans son
état fondamental (X 1Σg)
et dans deux états excités, notés respectivement H2*
(B 1Σu+)
et H2** (C 1Πu).
Déterminez les valeurs des paramètres re,
Te,
ωe,
ωexe,
Be
et  00
pour les deux états excités de la molécule. Corrigé 00
pour les deux états excités de la molécule. Corrigé
-
La page
6 de VR Molécules présente deux des premiers états excités de la molécule
de dihélium, He2 soit He2* (A 1Σu+)
et He2** (C 1Σg);
l'état fondamental de la molécule est instable. Déterminez les valeurs
des paramètres re,
ωe,
ωexe,
Be et
l'énergie de transition  00
entre les deux états. Corrigé 00
entre les deux états. Corrigé
-
Revoyez l'animation
de la figure 5.8. En faisant apparaître les fenêtres (bouton
au bas, à gauche) qui illustrent la variation de longueur de liaison
associée aux divers niveaux de vibration, et en faisant varier ces
derniers pour les deux combinaisons d'états de chaque molécule, décrivez
les conditions qui rendent possibles ou favorisent les transitions
entre ces états électroniques et l'état fondamental des molécules
CO et H2. Corrigé
Corrigés
-
-
La différence d'énergie entre deux
niveaux est donnée par la relation 5.7 :
 υ'υ = υ'υ =  00 + ωe' υ' – ωe υ – ωe' xe' (υ' 2 + υ') + ωexe (υ2 + υ) 00 + ωe' υ' – ωe υ – ωe' xe' (υ' 2 + υ') + ωexe (υ2 + υ)
On peut donc construire le tableau
qui suit :
|
υ'
→ υ |
 |
Énergie (cm–1) |
| 1'
→0 |
 00 + ωe' – 2 ωe' xe' 00 + ωe' – 2 ωe' xe' |
66
227 |
| 2'
→1 |
 00 + 2 ωe' – 6 ωe' xe' – ωe + 2
ωexe 00 + 2 ωe' – 6 ωe' xe' – ωe + 2
ωexe |
65
532 |
| 3'
→
2 |
 00 + 3 ωe' – 12 ωe' xe' – 2
ωe + 6 ωexe 00 + 3 ωe' – 12 ωe' xe' – 2
ωe + 6 ωexe |
64
829 |
| 4'
→
3 |
 00 + 4 ωe' – 20 ωe' xe' – 3
ωe + 12 ωexe 00 + 4 ωe' – 20 ωe' xe' – 3
ωe + 12 ωexe |
64
118 |
| 5'
→
4 |
 00 + 5 ωe' – 30 ωe' xe' –
4 ωe + 20 ωexe 00 + 5 ωe' – 30 ωe' xe' –
4 ωe + 20 ωexe |
63
399 |
La première différence d'énergie
devient :
| |
Première
différence |
ΔE
(cm–1) |
| a |
ωe' – 4 ωe' xe' – ωe + 2 ωexe |
–
695 |
| b |
ωe' – 6 ωe' xe' – ωe + 4 ωexe |
– 703 |
| c |
ωe' – 8 ωe' xe' – ωe + 6 ωexe |
–
711 |
| d |
ωe' – 10 ωe' xe' – ωe + 8 ωexe |
–
719 |
La deuxième différence d'énergie
devient :
| |
Deuxième différence |
Δ[ΔE
(cm–1)] |
| a' |
– 2 ωe' xe' + 2 ωexe |
– 8 |
| b' |
– 2 ωe' xe' + 2 ωexe |
– 8 |
| c' |
– 2 ωe' xe' + 2 ωexe |
– 8 |
Puisque ωexe = 13,5
cm–1,
⇒ – 2 ωe' xe' + 2 ωexe = –
8 cm–1 et
ωe' xe' =
17,5 cm–1
En utilisant l'une des nombreuses
relations qui précèdent, la ligne a du tableau des premières
différences, par exemple, on obtient :
ωe' – 4 ωe' xe' – ωe + 2 ωexe = – 695
cm– 1
et
ωe' = – 695 +
4 × 17,5 +
2 170,2 – 27
ωe' = 1 518,2 cm–1
-
Le calcul de l'énergie de la transition
électronique pure est maintenant possible. En prenant la première
bande, on obtient :
 00 + ωe' – 2 ωe' xe' = 66 227 cm–1 00 + ωe' – 2 ωe' xe' = 66 227 cm–1
 00 =
64 744 cm–1 00 =
64 744 cm–1
-
L'énergie de dissociation s'obtient
en utilisant la formule de Birge-Spooner :
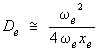
En remplaçant chaque valeur, on
obtient :
De
= 87 218 cm–1
et De' = 32
928 cm–1
-
L'énergie de dissociation chimique
D0
s'obtient simplement à partir des valeurs calculées en c. Pour
l'état fondamental, on trouve :
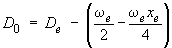
D0 = 87
218 – 1085,1 + 3,4 cm–1
D0 =
86 136,3 cm–1
Et pour l'état électronique
excité :
D0' = 32
173,3 cm–1
-
-
L'énergie de la bande est la différence
d'énergie entre deux niveaux de vibration des états excité et
fondamental. Elle est donnée par la relation 5.7 :
 υ'υ = υ'υ =  00 + ωe' υ' – ωe υ – ωe' xe' (υ' 2 + υ') + ωexe (υ2 + υ) 00 + ωe' υ' – ωe υ – ωe' xe' (υ' 2 + υ') + ωexe (υ2 + υ)
1er cas d'espèce
Regardons à l'intérieur d'une colonne.
La valeur de υ demeure constante
et la variable est υ'.
Par conséquent, la valeur de l'énergie d'une transition entre
un niveau quelconque υ'
de l'état électronique excité et un niveau υ
de l'état fondamental est :
 υ'υ =
b + (ωe'
– ωe' xe')
υ' –
ωe' xe' υ' 2 υ'υ =
b + (ωe'
– ωe' xe')
υ' –
ωe' xe' υ' 2
avec
b =  00 - ωeυ + ωexe (υ 2 + υ) 00 - ωeυ + ωexe (υ 2 + υ)
La résolution de l'équation quadratique
est y
= 0,0476 x2
+ 150,02 x
+ 30 308 avec un coefficient de corrélation de 1,00. On observe
que la valeur du coefficient de υ' 2
est ωe' xe'
. Ce coefficient est voisin de 0 cm–1. Cette
valeur est confirmée visuellement par la moyenne observée de la
seconde différence. Dans ces conditions, le coefficient de υ'
est égal à ωe'.
La valeur de ωe'
est donc égale à 150,02 cm–1. La valeur
moyenne (arithmétique) de la première différence observée dans
le tableau est de 149,75 cm–1.
On peut répéter les mêmes calculs
pour les deux autres colonnes. On retrouve les mêmes observations
: y
= 0,1905 x2
+ 147,93 x
+ 30 113 avec R2
= 1,0. Le coefficient de υ' 2
est voisin de 0 cm–1. La valeur de ωe'
est donc égale à 147,93 cm–1.
Pour la troisième colonne, y
= -0,2591 x2
+ 150,43 x
+ 29 912 avec R2
= 1,0. Le coefficient de υ' 2
est toujours voisin de 0 cm–1. La valeur
de ωe'
est donc égale à 150,43 cm–1.
En moyenne, ωe'
est donc égal à (150,02 + 147,93 + 150,43) / 3 = 149,46 cm–1.
De la même manière le coefficient b
est égal à : 30 308, 30 113 et 29 992 cm–1
pour chacune des trois colonnes concernées.
-
2e cas d'espèce
Regardons maintenant les résultats
de ce tableau, ligne par ligne. La valeur de υ
ne demeure plus constante : ce sera la variable. La constante
est maintenant υ'. Par conséquent,
l'examen de ce tableau devrait donner les valeurs de ωe
et de ωexe.
L'énergie d'une bande quelconque est :
 υ'υ = υ'υ =  00 + ωe' υ' – ωe υ – ωe' xe' (υ' 2 + υ') + ωexe (υ2 + υ) 00 + ωe' υ' – ωe υ – ωe' xe' (υ' 2 + υ') + ωexe (υ2 + υ)
Soit encore :
 υ'υ =
a – ωe υ + ωexe (υ2 + υ) υ'υ =
a – ωe υ + ωexe (υ2 + υ)
avec a =  00 + ωe' υ' – ωe' xe' (υ' 2 + υ') 00 + ωe' υ' – ωe' xe' (υ' 2 + υ')
De nouveau les équations quadratiques
montrent que les valeurs de ωexe
sont
voisines de la valeur 0. Dans chacune des quatre courbes, on trouve
les valeurs de ωe
suivantes : 197,98; 197,93; 196,67 et 200,77 cm–1,
soit une valeur moyenne de 198,34 cm–1.
Quant aux valeurs de la constante a,
elles sont : 30 310, 30 457, 30 606 et 30 758
cm–1 pour chacune des lignes concernées.
-
Connaissant les valeurs de ωe
et ωe'
(ωexe
et ωe' xe'
sont égales à 0) obtenues
plus haut, on peut, connaissant les valeurs de a
et de b
dans chacune des colonnes et des lignes, obtenir une valeur de
la transition électronique pure,  00. 00.
 00 = a
– ωe' υ'
et 00 = a
– ωe' υ'
et  00 = b + ωe υ 00 = b + ωe υ
| υ' |
a
(cm–1) |
ωe'
(cm–1) |
 00 00
(cm–1) |
υ |
b
(cm–1) |
ωe
(cm–1) |
 00 00
(cm–1) |
| 0 |
30 310 |
149,46 |
30 310 |
0 |
30 308 |
198,34 |
30 308 |
| 1 |
30 457 |
|
30 307,5 |
1 |
30 113 |
|
30 311,3 |
| 2 |
30 606 |
|
30 307,8 |
2 |
29 912 |
|
30 308,6 |
| 3 |
30 758 |
|
30 309,6 |
|
|
|
|
On obtient ainsi sept valeurs de
l'énergie de la transition électronique pure. La moyenne de ces
valeurs est :
 00 = 30 309,0 cm–1 00 = 30 309,0 cm–1
-
-
On peut obtenir les valeurs de
ωe
et ωexe
en utilisant les trois premières
têtes de bande :
G(υ)
= ωe
(υ + 1/2) – ωexe
(υ + 1/2)2
G(0)
= ωe/2
– ωexe/4
G(1)
= ωe
(υ + 3/2) –
ωexe(9/4)
G(2)
= ωe
(υ + 5/2) – ωexe(25/4)
G(3)
= ωe
(υ + 7/2) –
ωexe(49/4)
La première différence devient
:
G(1)
– G(0) = ωe
– 2 ωexe
G(2) –
G(1) = ωe
– 4 ωexe
G(3) –
G(2) = ωe
– 6 ωexe
La deuxième différence devient
:
[G(2) –
G(1)] – [G(1) – G(0)] =
– 2 ωexe
[G(3) –
G(2)] – [G(2) – G(1)]
= – 2 ωexe
Exemple de calculs
Pour la première série, on obtient
:
G(0)
= ωe/2
– ωexe/4 = 0
cm–1
G(1) = ωe
(υ + 3/2) –
ωexe(9/4) = 1
556,4 cm–1
G(2) = ωe
(υ + 5/2) – ωexe(25/4) = 3
089,2 cm–1
Il faut tout de suite remarquer
que l'auteur utilise le niveau υ = 0
de l'état électronique fondamental comme référence et non pas
le minimum de la courbe de potentiel. Si les valeurs G(υ)
ne sont donc pas exactes, les différences, elles, le sont. Il
s'ensuit que :
G(1) –
G(0) = ωe
– 2 ωexe = 1
556,4 cm–1
G(2) – G(1) = ωe
– 2 ωexe = 1
532,8 cm–1
Et finalement :
[G(2) –
G(1)] – [G(1) – G(0)]
= – 2 ωexe = – 23,6
cm–1
ce qui permet d'obtenir la valeur
de ωexe :
ωexe =
11,8 cm–1
En utilisant la relation G(1)
–
G(0), on peut obtenir la valeur de
ωe :
ωe
= 2 ωexe + 1
556,4 cm–1
= 23,6 + 1 556,4
ωe
= 1 580,0 cm–1
On obtient ainsi les résultats
numériques affichés dans le tableau suivant :
| États
électroniques |
ωe
(cm–1) |
ωexe
(cm–1) |
De
(cm–1) |
G(0)
(cm–1) |
| X 3Σ |
1580,0 |
11,8 |
52 890,0 |
787,1 |
| a 1Δg |
1509,9 |
13,10 |
43 507,6 |
747,4 |
| b 1Σ |
1432,0 |
14,0 |
36 659,0 |
712,5 |
| c 1Σ |
770,3 |
14,75 |
10 057,0 |
381,5 |
| A' 3Δu |
762,0 |
17,05 |
8 514,0 |
376,8 |
| A 3Σ |
804,8 |
15,2 |
10 653,0 |
398,6 |
La valeur de l'énergie de dissociation
spectroscopique De
est donnée par l'équation de Birge-Spooner :
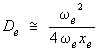
De la même manière, l'énergie du
point zéro G (0)
est donnée, en cm–1, par la relation :
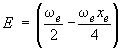
Ces valeurs complètent le tableau
précédent.
-
L'état fondamental X 3Σ
se traite aisément par voie électronique puisque la relation qui
existe entre l'énergie d'un niveau de vibration et le nombre quantique
vibrationnel, υ, est telle
que :
 = d
+ b k – c k2 = d
+ ωeυ
– ωexeυ2 =
E (cm–1) = d
+ b k – c k2 = d
+ ωeυ
– ωexeυ2 =
E (cm–1)
Le traitement électronique donne
les résultats suivants (dans chacun des cas R2
est voisin de 1,000) :
ordre 2 : y = –
11,402 x2 + 1566,3 x + 1,4519
ordre 3 : y = +
0,0093 x3 – 11,597 x2
+ 1567,3 x + 0,4395
ordre 4 : y
= – 0,0013 x4 + 0,0449
x3 – 11,911 x2 + 1568,2
x + 0,0034
Remarque : la courbe passe par
une valeur proche de zéro à l'origine du graphe. Par conséquent,
au fur et à mesure que l'on augmente l'ordre ou la puissance du
polynôme, on augmente la concordance au point zéro du graphe.
La courbe du deuxième degré ne tient compte que du nombre quantique
de vibration. La courbe du 3e degré introduit
un terme, une correction liée à la déformation subie par la molécule
dans son mouvement de rotation. La courbe du 4e degré
introduit une autre correction que l'on peut rattacher à la constante
de distorsion centrifuge.
Dans le cas de la réaction d'ordre
2, ωe = 1566,3
cm–1 et ωexe = 11,402 cm–1.
Cela permet de calculer une valeur De = 53 790,22 cm–1
Dans le cas de la réaction d'ordre
3, ωe = 1567,3
cm–1 et ωexe = 11,597 cm–1.
Cela permet de calculer une valeur De = 52 985,96 cm–1
Dans le cas de la réaction d'ordre
4, ωe = 1568,2 cm–1
et ωexe = 11,911 cm–1.
Cela permet de calculer une valeur De = 51 624,85 cm–1.
Ces trois équations permettent
d'apprécier la sensibilité de l'approche. On peut comparer les
valeurs de ωe
et de ωexe
avec les valeurs obtenues via la 1re et la 2e différence.
Notons que dans d'autres cas, le mouvement de rotation et la constante
de distorsion centrifuge introduisent des perturbations plus importantes.
| États
électroniques |
ωe (cm–1) |
ωexe
(cm–1) |
| 1re
et 2e différences |
Polynôme
ordre 2 |
Polynôme
ordre 3 |
1re
et 2e différences |
Polynôme
ordre 2 |
Polynôme
ordre 3 |
| X
3Σ |
1580,0 |
1566,3 |
1567,3 |
11,6 |
11,4 |
11,6 |
| a
1Δg |
1509,9 |
1498,6 |
1496,1 |
13,1 |
13,4 |
12,75 |
| b
1Σ |
1432,0 |
1418,8 |
1418,8 |
14,0 |
14,0 |
14,0 |
| c
1Σ |
770,3 |
783,3 |
755,7 |
14,75 |
18,95 |
14,2 |
| A' 3Δu |
762,0 |
783,2 |
735,75 |
17,05 |
25,4 |
11,5 |
| A
3Σ |
804,8 |
848,4 |
768,5 |
15,2 |
25,3 |
6,3 |
Les valeurs des niveaux de vibration
(cm–1) de divers états électroniques de l'oxygène
moléculaire apparaissent dans le tableau suivant :
|
υ |
A 3Σu+
|
c 1Σu– |
a 1Δg–
|
X 3Σg– |
b 1Σg+
|
A'
3Δu |
|
0 |
35 010,19 |
|
7 889,43 |
0 |
13 122,24 |
|
|
1 |
35 784,61 |
33 434,03 |
9 373,08 |
1 556,39 |
14 527,00 |
|
|
2 |
36 526,57 |
34 174,81 |
10 830,62 |
3 089,19 |
15 903,75 |
35
933,06 |
|
3 |
37 239,64 |
34 886,07 |
12 262,02 |
4 598,65 |
17 252,48 |
36
660,96 |
|
4 |
37 914,94 |
35 566,54 |
13 667,14 |
6 084,96 |
18 573,20 |
37
354,76 |
|
5 |
38 551,02 |
36 215,06 |
15 045,85 |
7 548,27 |
19 865,91 |
38
011,03 |
|
6 |
39 143,30 |
36 830,30 |
16 397,86 |
8 988,73 |
21 130,61 |
38
626,12 |
|
7 |
39 686,03 |
37 410,96 |
17 722,82 |
10 406,42 |
22 367,30 |
39
195,35 |
|
8 |
40 171,58 |
37 955,60 |
19 020,50 |
11 801,46 |
|
39
712,84 |
|
9 |
40 589,52 |
38 462,80 |
20 290,50 |
13 173,80 |
|
40
171,10 |
|
10 |
40 925,75 |
38 931,15 |
21 532,26 |
14 523,53 |
|
40
561,18 |
|
11 |
41 160,45 |
39 359,48 |
|
15 850,60 |
|
40
872,65 |
|
12 |
|
39 746,58 |
|
17 154,96 |
|
|
|
13 |
|
40 091,26 |
|
18 436,53 |
|
|
|
14 |
|
40 392,65 |
|
19 695,20 |
|
|
|
15 |
|
40 649,98 |
|
|
|
|
|
16 |
|
40 861,95 |
|
|
|
|
Les calculs précédemment faits
pour l'état fondamental peuvent être repris pour chacun des cinq
autres états électroniques identifiés. On obtient les résultats
consignés dans les tableaux qui suivent :
| États
électroniques |
Puissance
du polynôme |
d
(cm–1) |
| a 1Δg– |
2
3
4 |
7 888,0
7 889,6
7 889,4 |
| B 1Σg+ |
2
3
4 |
13 122
13 122
13 122 |
| c 1Σu– |
2
3
4 |
33 405
33 434
33 434 |
| A' 3Δu |
2
3
4 |
35 909
35 935
35 933 |
| A 3Σu+ |
2
3
4 |
34 961
35 018
35 009 |
L'ordonnée à l'origine correspond
à la transition vibrationnelle pure (le terme spectral électronique).
Dans chacun des cas, l'ordonnée à l'origine reste pratiquement
inchangée quand on passe d'un polynôme d'ordre 3 à un polynôme
d'ordre 4.
-
| États
électroniques |
Puissance
du polynôme |
ωe
(cm–1) |
ωexe
(cm–1) |
De
(cm–1) |
G (0)
(cm–1) |
| X 3Σg– |
2
3
4 |
1566,29
1567,3
568,25 |
11,402
11,59
11,91 |
53 790,22
52 985,96
51 624,85 |
780,29
780,75
781,15 |
| a 1Δg– |
2
3
4 |
1498,59
1496,09
1496,6 |
13,399
12,74
13,03 |
41 901,86
43 922,40
42 974,13 |
745,95
744,86
745,04 |
| b 1Σg+ |
2
3
4 |
1418,76
1418,77
1418,77 |
14,006
14,009
14,008 |
35 928,89
35 921,71
35 924,26 |
705,88
705,88
705,88 |
| c 1Σu– |
2
3
4 |
821,20
783,44
780,80 |
18,95
13,56
12,91 |
8 896,69
11 315,97
11 805,74 |
405,86
388,33
387,17 |
| A'
3Δu |
2
3
4 |
783,2
735,75
745,34 |
25,40
11,50
16,88 |
6 037,4
11 768,0
8 227,7 |
385,25
365,00
368,45 |
| A 3Σu+ |
2
3
4 |
848,42
768,5
793,9 |
25,34
6,36
17,80 |
7 105,6
23 215,1
8 852,2 |
417,88
382,66
392,50 |
On peut voir que dans les deux
derniers cas, la fluctuation des résultats est relativement grande
lorsque varie la puissance du polynôme. Finalement, ces résultats
numériques peuvent être comparés aux résultats obtenus simplement
en prenant les trois premières bandes pour le calcul de ωe
et de ωexe.
Les valeurs de ωe
obtenues par le calcul électronique sont plus élevées et il en
est de même des valeurs de De
et de G (0).
Certaines de ces courbes de potentiel
apparaissent à la figure
5.2.
Corrigés des problèmes avec VR Molécules
-
re
se mesure directement à l'aide de la grille;
ωe
est égal au double de l'énergie de vibration du niveau υ = 0;
ωexe
est égal à la différence d'énergie du niveau υ = 5
avec et sans anharmonicité, divisée par (5 + 1/2)2;
Be est
égal à la moitié de l'énergie de rotation du niveau J = 1;
Te
est égal à la différence d'énergie totale entre les deux états
quand leur énergie de vibration est mise à zéro;
 00
est égal à la différence des énergies totales des deux états dans
leur niveau fondamental de vibration υ = 0. 00
est égal à la différence des énergies totales des deux états dans
leur niveau fondamental de vibration υ = 0.
On trouve les résultats suivants :
| État |
re
(pm) |
ωe
(cm–1) |
ωexe
(cm–1) |
Be
(cm–1) |
Te
(cm–1) |
 00 00
(cm–1) |
| I2 |
270 |
214,5 |
0,62 |
0,037 |
0 |
– |
| I2* |
304 |
125,7 |
0,75 |
0,029 |
15 769 |
15 725 |
-
Les quantités sont déterminées de
la même façon qu'en 1. On trouve :
| État |
re
(pm) |
ωe
(cm–1) |
ωexe
(cm–1) |
Be
(cm–1) |
Te
(cm–1) |
 00 00
(cm–1) |
| H2* |
130 |
1358,1 |
20,89 |
20,01 |
91 700 |
99 120 |
| H2** |
104 |
2443,8 |
69,5 |
31,36 |
100 090 |
100 103 |
-
Les quantités sont déterminées toujours
de la même façon. On trouve :
| État |
re
(pm) |
ωe
(cm–1) |
ωexe
(cm–1) |
Be
(cm–1) |
Te
(cm–1) |
 00 00
(cm–1) |
| He2** |
110 |
1653,4 |
41,0 |
7,052 |
157 415 |
10 944 |
-
Molécule CO, état excité CO* (a 3Πr).
Il y a un certain chevauchement entre les niveaux fondamentaux. Ce
chevauchement augmente avec les nombres quantiques; il est déjà assez
important pour υ = 2.
Molécule CO, état excité CO** (A 1Π).
Il y a un certain chevauchement entre les niveaux fondamentaux, mais
moins important que précédemment. Ce chevauchement augmente avec les
nombres quantiques; il est déjà assez important pour υ = 4.
Molécule H2, état excité H2*
(B 1Σu+).
Il n'y a aucun chevauchement entre les niveaux fondamentaux. Le chevauchement
ne débute qu'avec des nombres quantiques relativement élevés (de l'ordre
de 10) et ne devient jamais important.
Molécule H2, état excité H2**
(C 1Πu).
Il n'y a aucun chevauchement entre les niveaux fondamentaux. Le chevauchement
ne débute qu'avec des nombres quantiques relativement élevés (de l'ordre
de 7) et ne devient important qu'à des nombres quantiques proches
de la dissociation (de l'ordre de 15).
|



