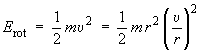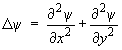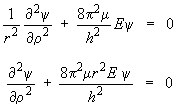|
|
|
|
MODULE 1 Rotation des
molécules diatomiques Préambule La molécule diatomique, la plus simple, peut tourner sur elle-même. Comment peut-on observer ce mouvement moléculaire? Est-ce que l’application de la mécanique classique renseigne sur les lois qui gouvernent ce mouvement? L’introduction de la mécanique quantique est-elle nécessaire? Si oui, quelles en sont les conséquences sur l’interprétation des observations? Une molécule est un objet comme un autre. Elle est donc susceptible de tourner sur elle-même, comme une toupie. Voyons comment le mouvement de rotation s’exprime avec les molécules les plus simples, soit les molécules diatomiques. Les molécules possèdent un autre type de mouvement interne : la vibration. Ce mouvement est étudié dans le module 2.
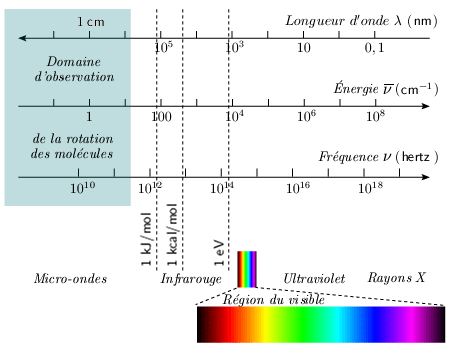
Faits expérimentaux Lorsqu'on fait de l'absorption dans l'infrarouge lointain, au-delà de 30 μm, on observe, pour une molécule donnée, une série de raies d'absorption à peu près équidistantes. Des spectres d'absorption analogues sont également observés dans la région des hyperfréquences (longueur d'onde dans la région de 0,2 à 2 mm). La position du spectre d'absorption dans l'échelle des longueurs d'onde dépend de la molécule étudiée. En général, plus la molécule est lourde, plus le spectre se trouve dans une région de grande longueur d'onde (figure 1.1.).
Nous étudierons maintenant la rotation d’une manière quantitative, en prenant comme exemple la molécule de chlorure d'hydrogène, HCl. La première colonne du tableau 1.1 présente, à titre d'exemple, les fréquences d'absorption (exprimées en nombre d'ondes) observées pour la molécule HCl (gazeux). Le spectre de cette molécule se trouve dans le domaine infrarouge lointain accessible aux spectromètres infrarouges optiques. Tableau 1.1.
Fréquences d'absorption dans
m est un nombre entier. Nous montrerons plus loin que ce spectre peut être interprété comme une transformation de l'énergie électromagnétique absorbée en énergie de rotation. Notons que l'absorption n'est pas continue; cela signifie que certains états énergétiques seulement sont possibles dans la rotation et que la molécule passe brusquement (par quanta) d'un état à l'autre. L'émission d'énergie par le même processus ne peut s'observer que si un très grand nombre de molécules émettrices sont présentes. C’est le cas en radio-astronomie, où certains corps célestes émettent ce type de rayonnement (détecté par les radio-télescopes) à partir des molécules diatomiques qui y sont présentes, révélant du même coup au moins une partie de leur composition.
Modèle mécanique - le rotateur rigide symétrique Examinons un modèle mécanique simple d’une molécule diatomique, soit le rotateur rigide. Soulignons que toute représentation d’un objet quantique comme une molécule à l’aide de modèles classiques tels que celui illustré à la figure 1.2, appelle à la prudence. En effet, de tels modèles fournissent de ces objets une représentation utile (on dirait pédagogique) de leurs mouvements, mais cette représentation est toujours partielle, voire même inexacte.
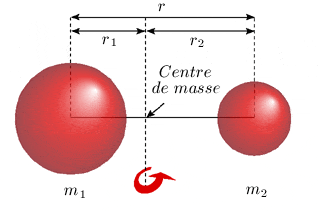
En mécanique classique, un système isolé, c'est-à-dire non soumis à des forces externes, ne peut tourner qu'autour d'un point appelé centre de masse. La position de ce point est telle que la somme vectorielle des moments (le produit du vecteur position par la masse) de chacune des composantes du système, par rapport à ce point, est nulle. Selon notre modèle, chacun des deux atomes de masse m1 et m2 est supposé réduit à un point matériel, ce qui est sûrement une bonne approximation quand on considère (Voir Chimie théorique, chapitre 2, section 3) que la quasi-totalité de la masse d’un atome est concentrée dans son noyau qui est beaucoup plus petit que son nuage électronique illustré à la figure 1.2. On néglige l'effet de la gravité, de même que la masse des électrons. On imagine également que les deux atomes sont liés de façon rigide, comme par une barre de masse négligeable. Avec ces hypothèses simplificatrices, la position du centre de masse d'une molécule diatomique est décrite par l'égalité suivante :
où r1 et r2 sont les distances respectives des atomes 1 et 2 au centre de masse. Mais on a, d'après la figure 1.2 : r1 = r – r2 et r2 = r – r1 ce qui permet de récrire l'expression 1.1a des deux manières suivantes : m1r1 = m2(r – r1) et m2r2 = m1(r – r2) Transformons maintenant ces deux expressions de la façon suivante : m1r1 + m2r1 = m2r et m2r2 + m1r2 = m1r On en tire:
En vertu des mêmes hypothèses, le seul moment d'inertie non nul est le moment par rapport à un axe perpendiculaire à l'axe internucléaire. La seule rotation que l'on doit considérer est donc celle qui s'effectue autour de cet axe et le moment d'inertie I de la molécule est donné par : I = m1 r12 + m2 r22 En substituant dans cette équation les expressions de r1 et r2 données en 1.1b, on obtient :
μ est appelé la masse réduite de la molécule. Les expressions 1.1c signifient que, du point de vue de la mécanique, la molécule diatomique peut être étudiée comme un atome unique de masse μ tournant autour d'un point situé à la distance fixe r égale à la distance internucléaire. C'est ce qu'illustre l'animation de la figure 1.3. que vous pouvez observer dans la fenêtre d'animation en cliquant dans la figure.
On peut envisager deux cas limites.
On voit donc que dans tous les cas la masse réduite μ est telle que m1/2 < μ < m1; elle est comprise entre la moitié et la valeur entière de la masse de l'atome le plus léger. On peut aussi examiner l'influence relative de chacune des deux masses sur la position du centre de masse.
Note. Pour que l'animation s'affiche à la page indiquée ci-dessus, vous devez cliquer sur l'onglet portant ce numéro au bas de l'écran de VR Molécules. Voyons comment exprimer mathématiquement la relation entre la vitesse de rotation, l’énergie et la masse réduite d’un rotateur rigide. L'énergie du système est essentiellement son énergie cinétique de rotation :
υ est la vitesse tangentielle.
Mais comme m doit être identifié
à μ, et sachant que ω, la
vitesse angulaire, est égale à υ/r,
on peut écrire :
ou encore, comme le moment cinétique peut s'écrire : P
= I ω L'énergie
s'exprime finalement comme :
En théorie classique, l'énergie du système peut prendre une valeur quelconque dépendant du moment cinétique, c'est-à-dire de la vitesse de rotation.
Traitement quantique du modèle mécanique Le modèle mécanique classique ne permet pas d'aller plus loin et, en particulier, ne permet pas de déterminer les états énergétiques possibles. La méthode quantique appliquée au mouvement de l'électron autour du proton (Voir Introduction à la physique atomique et nucléaire, chapitre 6, section 4) est également applicable au mouvement des noyaux. On peut déterminer, à l'aide de la mécanique quantique, une fonction d'onde ψsolution de l'équation générale de Schrödinger. Le carré de cette fonction d'onde représentera la probabilité de présence des noyaux en chaque point de l'espace. Dans le cas du rotateur rigide symétrique, l'énergie potentielle V = 0 et l'équation d'onde de Schrödinger devient :
ψest la fonction d'onde, E l'énergie du rotateur, μ la masse réduite et h la constante de Planck. La solution de cette équation est possible de façon rigoureuse. Bien qu'elle ne soit pas nécessairement très compliquée, elle est cependant hors des limites de ce module. Si l'on veut que ψ réponde aux conditions physiques que l'on s'est imposées, c'est-à-dire ait le caractère d'une onde, l'énergie E peut seulement prendre les valeurs suivantes (Voir Introduction à la physique atomique et nucléaire, chapitre 2, section 2.3) :
J est un nombre quantique de rotation qui peut prendre les valeurs : J = 0, 1, 2, ... Ouvrons une parenthèse pour essayer de mieux faire comprendre comment l'équation de Schrödinger fournit ce résultat. L'intégration de l'équation est très facile si on l'applique au rotateur rigide à axe fixe (figure 1.3). Ce problème pourrait être matérialisé par une molécule astreinte à tourner autour d'un axe en restant dans un plan, par exemple le plan xy. Dans ce cas, le laplacien Δψ de la fonction d'onde se réduit à :
Étant donné la symétrie du problème, il est préférable de le traiter en coordonnées polaires. Après un changement de coordonnées, l'expression précédente s'écrit :
ρ est l'angle que fait la molécule avec une direction origine fixe (c'est la seule variable du problème); r est la distance fixe de la masse μ à l'axe de rotation. L'équation devient donc :
Cette équation aux dérivées partielles du second ordre à coefficients constants a pour solution générale (voir Introduction à la physique atomique et nucléaire, chapitre 6, section 4) : ψ = c1 cos Jρ + c2 sin Jρ
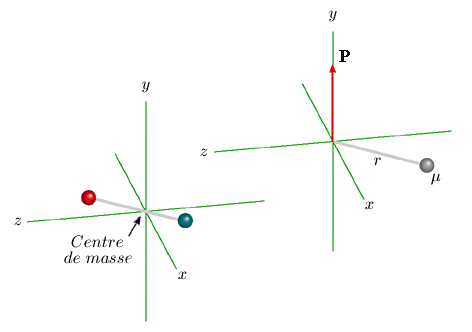
Cependant, cette fonction d'onde ψ n'est satisfaisante que si les conditions aux limites sont satisfaites. En particulier, la fonction ψdoit être continue c'est-à-dire qu'elle doit prendre les mêmes valeurs pour ρ, ρ + 2 π, ρ + 4 π, etc. correspondant au même point de l'espace. Cette condition impose que le nombre J soit entier. L'équation 1.4 donne donc la condition correspondante à satisfaire pour l'énergie. On a donc des valeurs discrètes de l'énergie, données par : E = (h2 / 8π2I ) J 2 C'est une condition presque analogue que l'on retrouve dans le cas du rotateur rigide symétrique (équation 1.3). Le rotateur à axe fixe orienté selon l'axe z peut être considéré comme un modèle approché de notre molécule. Cependant, un modèle plus exact, fondé sur la solution complète de l'équation de Schrödinger, montre que l'axe de rotation de la molécule ne peut être parallèle à aucun des axes. C'est là l'origine du facteur J (J + 1) (au lieu de J 2) dans l'expression de E (équation 1.3). Cette propriété se manifeste, entre autres, en présence d'un champ électrique. Si on suppose ce dernier orienté selon l'axe z, on peut représenter le mouvement de la molécule comme la combinaison de deux mouvements : (1) la rotation de la molécule autour de son axe; (2) la rotation, plus lente, de cet axe autour de l'axe z, mouvement appelé précession. C'est ce qu'illustre l'animation de la figure 1.4., qui montre comment évolue le vecteur moment cinétique P, parallèle à l'axe de rotation de la molécule.
Les niveaux d'énergie de la molécule en rotation En comparant l'équation 1.3 et l'équation 1.1c on peut écrire : I = μr2 E = 1/2 I ω2 = 1/2 (I ω)2 / I = 1/2 P 2 / I D'où : P 2 = 2 E I = 2 (h2I /8 π2I ) J (J + 1) Ce qui permet d'écrire:
Cette équation montre que le nombre quantique J détermine la grandeur du moment cinétique P. Comme dans le cas d'un électron tournant autour du noyau, c'est le moment cinétique qui est quantifié, c'est-à-dire ne peut varier que par quanta approximativement égaux à h / 2π, car :
Puisque l'énergie se manifeste sous
forme électromagnétique,
caractérisons-la par sa fréquence ν
ou par son nombre d'ondes E = hν
= hc Posons E = hc F(J) D'après l'équation 1.3 nous trouvons :
La constante B est appelée constante de rotation de la molécule; F(J) est le terme spectral : c'est la position du niveau d'énergie exprimée en nombre d'ondes.
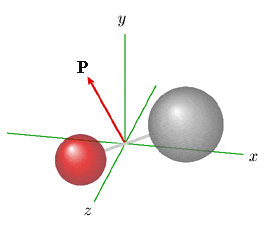
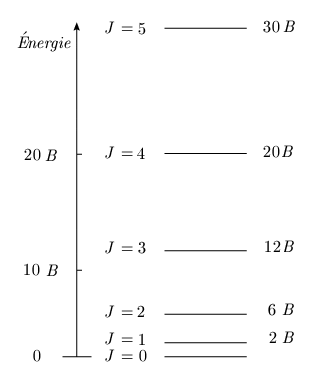
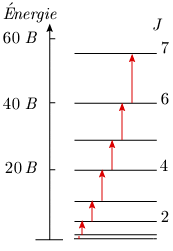
Le diagramme de niveaux d'énergie de la molécule en rotation apparaît comme une série de lignes horizontales représentant les niveaux possibles (figure 1.5.). Ces niveaux d'énergie possibles correspondent aux valeurs J = 0, 1, 2, ... Ils s'écartent de plus en plus les uns des autres puisque l'énergie varie suivant une loi quadratique; la séparation de deux niveaux consécutifs est donnée par (voir la section Spectre de rotation) :
Cette différence croît avec J.
Transitions possibles d'un niveau d'énergie à l'autre L'émission et l'absorption d'énergie électromagnétique ne peut se faire que si elle est accompagnée d'une variation de moment dipolaire électrique à l'intérieur du système émetteur (Voir Introduction à la physique atomique et nucléaire, chapitre 6, section 4). Une variation de moment dipolaire électrique c'est, pour parler plus simplement, un déplacement du centre de gravité des charges; rappelons que si la distance du centre de gravité des charges positives, +q, au centre de gravité des charges négatives, –q, est d, le moment dipolaire électrique est défini par le produit qd. Il découle immédiatement de ces remarques que les molécules diatomiques homonucléaires ne possèdent pas de spectre de rotation par suite de l'absence de moment dipolaire. Cela ne signifie pas que ces molécules ne peuvent entrer en rotation ou qu'elles ne peuvent accumuler ou perdre de l'énergie de rotation. Il existe d'autres mécanismes (voir module 4) capables d'enrichir (ou d'appauvrir) l'énergie de rotation de ces molécules homonucléaires. En ce qui concerne les molécules hétéronucléaires, une transition ne sera possible entre deux niveaux d'énergie que si le moment dipolaire varie. On démontre que cette condition impose à J de varier de ±1. On aboutit donc à une règle de sélection pour les transitions de rotation :
Dans le cas de l'absorption, un quantum d'énergie porte la molécule à un niveau plus élevé, donc les seules transitions possibles sont : ΔJ = Jfinal – Jinitial = +1 Ce serait ΔJ = –1 dans le cas de l'émission. Sur le diagramme de niveaux d'énergie (figure 1.6) on a représenté les transitions possibles par des flèches, chacune d'elles donnant lieu à la présence d'une raie dans le spectre d'absorption.
Spectre de rotation et calcul des constantes moléculaires Calculons l'énergie d'une raie quelconque. Cette raie correspond à une transition entre deux niveaux J et J + 1. D'après l'équation 1.6, la différence d'énergie entre deux niveaux successifs est :
Cette formule est la démonstration théorique de la formule empirique :
La raie suivante correspond à la transition (J + 1) → (J + 2). Sa fréquence est :
L'intervalle des fréquences entre deux raies consécutives est constant :
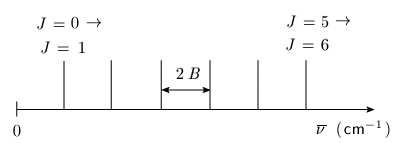
On observe ainsi un spectre que l'on peut schématiser comme cela est fait dans la figure 1.7. Il faut noter que l'on ne traite pas ici des intensités des raies d'absorption (hauteur des pics).
De la valeur expérimentale de cette différence on peut tirer la valeur de B. Par exemple, dans le cas de HCl, on trouve : B = 20,68 / 2 = 10,34 cm–1 À partir de la valeur de B on peut déduire la valeur du moment d'inertie de la molécule, par la relation 1.6 :
On peut ensuite, connaissant les masses des atomes, utiliser l'équation 1.1c pour déterminer la distance internucléaire.
Signification physique des nombres J et B J détermine la valeur du moment cinétique. La molécule tourne comme une toupie autour de l'axe. Les valeurs croissantes de J correspondent à des valeurs croissantes de la fréquence de rotation, donc de la vitesse angulaire de rotation. La grandeur B est liée directement au moment d'inertie de la molécule. Voici quelques ordres de grandeur pour des molécules diatomiques communément rencontrées. Tableau 1.2. Quelques caractéristiques physiques de molécules biatomiques.
Correction pour la force centrifuge
On conçoit aisément, puisque la liaison entre les atomes n’est pas réellement rigide, que la force centrifuge imposée aux atomes est susceptible d'augmenter la longueur de cette liaison. Or, si B croît, la molécule tourne de plus en plus vite, donc la force centrifuge augmente, ce qui fait augmenter la longueur de la liaison, r, et par conséquent la valeur du moment d'inertie, car I = μr2. Puisque (équation 1.6) :
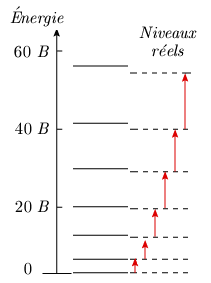
cette augmentation de I entraîne la décroissance de B. En conséquence, les niveaux d’énergie de rotation seront un petit peu plus rapprochés (figure 1.8.) que les niveaux théoriques prévus par la formule : F (J) = BJ (J +1) Celle-ci peut être corrigée, pour tenir compte de la force centrifuge, de la façon suivante :
En supposant que D = 0,5 × 10–4 B (cas de HCl), pour une valeur de J = 20, la correction est de 4 %. Cette correction atteint 9 % pour J = 30. Il faut donc observer des niveaux de rotation relativement élevés ou encore utiliser des appareils de mesure doués de très haute résolution pour apprécier la différence. Les exemples rapportés dans le tableau 1.3 montrent la pertinence de cette remarque.
Tableau 1.3. Quelques
constantes de distorsion
La relation entre la vitesse de rotation et la fréquence de la transition La question que l'on peut se poser est celle relative à la relation qui existe entre la vitesse de la rotation, la vitesse angulaire et la fréquence de la transition de rotation. Rappelons que, dans le système international d'unités (SI), la vitesse angulaire s'exprime en radians par seconde, rad/s. Comme le radian est une unité sans dimension, ces unités sont équivalentes à des s-1, soit la même unité qu'une fréquence d'absorption. La formule 1.2 relie l'énergie d'un niveau de rotation et le moment cinétique P. Cette dernière valeur est reliée à celle de la vitesse angulaire, ω, de telle sorte que: E = P 2 / 2I et P = I ω En se rappelant que E = hν, on obtient : E / h = P 2 / 2 I h = I 2ω2 / 2 I h = ν ou encore : ω2 = 2 hν / I Il n'existe donc pas de relation simple entre la vitesse angulaire de la rotation et la fréquence des raies d'absorption de rotation si ce n'est à travers une formule faisant intervenir le moment d'inertie de la molécule. On présente au module 2, consacré à la vibration, une situation quelque peu différente.
Conclusions L’application de la mécanique classique est insuffisante pour l’interprétation des observations spectroscopiques du mouvement de rotation des molécules diatomiques. Par contre, elle permet de mieux comprendre l’application de la mécanique quantique. Les molécules diatomiques ne peuvent tourner qu’avec des niveaux d’énergie quantifiés qui se traduisent par l’introduction d’un nombre quantique de rotation ainsi que par l’intervention de règles de sélection qui précisent les transitions possibles entre ces niveaux. Par ailleurs, l’interprétation du spectre observé dans l’infrarouge lointain permet de calculer avec une très grande précision la longueur de la liaison de la molécule.
Pour en savoir plus L'œuvre d'un Canadien, prix Nobel de chimie, toujours la référence fondamentale en spectroscopie moléculaire même après un demi-siècle : Herzberg, G. Molecular spectra and Molecular structure. I. Spectra of diatomic molecules. Van Nostrand Reinhold Company, Toronto, 1950, 658 pages. Liens utiles Une base de données, appelée WebBook, contenant, entre autres, les valeurs des constantes moléculaires (incluant les constantes de rotation B et D) des molécules diatomiques, est disponible sur le site du National Institute of Standards and Technology (NIST). On peut y faire une recherche par nom de molécule, ou encore à partir d'une liste de 400 molécules diatomiques, tirée des travaux de Huber et Herzberg. Une étude du mouvement de rotation de la molécule CO : Karol, P. J., Introduction to Modern Chemistry - Measuring Bond Lengths, Carnegie Mellon University, http://www.andrew.cmu.edu/course/09-105/RotationalSpectra.html Des explications théoriques et la description d'une expérience de laboratoire portant sur le spectre de HCl : Brucat, P. J. (1998). Physical Chemistry Laboratory - The Rotation / Vibration Spectrum of HCl, University of Florida Chemistry Dept., http://chem.ufl.edu/~itl/4411L_f00/hcl/hcl0.html [archive]. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||