MODULE 1 Rotation des
molécules diatomiques
Problèmes
- Calculez, en cm–1, la position (l'énergie) des quatre premières raies purement rotationnelles pour la molécule ClF (rCl–F = 163 pm), ainsi que la constante de distorsion centrifuge D = 0,5 × 10–4 B. On prendra 35 comme valeur pour la masse de l'atome de chlore. Corrigé
-
La molécule HF a des raies rotationnelles séparées de 41,9 cm–1. Calculez son moment d'inertie, la longueur de la liaison et sa vitesse angulaire dans les quatre premiers niveaux rotationnels. Corrigé
-
Si la longueur de la liaison H-Cl était multipliée par 10, sans altération de la masse de la molécule, le spectre d'absorption rotationnel serait-il altéré? Si oui, comment? Corrigé
-
La distance N–0 dans la molécule d'oxyde nitrique est de 115 pm.
- Calculez son moment d'inertie dans les systèmes C.G.S. et SI.
- Calculez l'énergie pour les niveaux de
rotation J = 1, 2, 3, 4 :
- En ergs/molécule;
- En cal/mole;
- En joules/mole.
- Calculez, en nombre d'ondes, la fréquence de la raie d'absorption lorsque J passe de 0 → 1, 1 → 2 et 2 → 3.
-
La constante rotationnelle B dans H35Cl est de 10,34 cm–1; calculez la valeur de la même constante dans H37Cl. Corrigé
-
A. Honig et autres [Phys. Rev., 96, 629 (1954)] ont étudié les spectres de rotation des halogénures alcalins. Le tableau suivant donne les valeurs qu'ils ont obtenues pour les transitions J = 8 → 9 entre les niveaux de rotation du bromure du rubidium gazeux, au niveau fondamental de vibration (υ = 0) :
Molécule
ν × 10–6 (s–1)
85Rb79Br
25 596,03 ± 0,10
87Rb79Br
25 312,99 ± 0,10
85Rb81Br
25 268,84 ± 0,10
où ν désigne la fréquence de la transition.
En supposant que la molécule RbBr se comporte comme un rotateur rigide, calculez, d'après les valeurs données ci-dessus, les distances internucléaires des molécules isotopes de RbBr, les masses atomiques des différents isotopes étant les suivants [T. L. Collins et autres, Phys.Rev., 94, 398 (1954)].79Br : 78,943 65 85Rb : 84,939 20
81Br : 80,942 32 87Rb : 86,937 09. -
Dans la série des composés diatomiques 1H–X proposés dans le tableau suivant, montrez théoriquement, en négligeant la masse de l'atome d'hydrogène devant celle de l'atome X, que la valeur de B est une fonction de 1 / re2. Vérifiez expérimentalement le résultat en traçant le graphe approprié. Corrigé
Molécule
État fondamental
B (cm–1)
re (nm)
1H–14N
X 3Σ–
16,699
0,103 62
1H–16O
X 2Πi
18,911
0,096 97
1H–19F
X 1Σ+
20,956
0,091 68
1H–24Mg
X 2Σ+
5,8257
0,172 97
1H–32S
X 2Πi
9,46
0,1341
1H–35Cl
X 1Σ+
10,593
0,1274
1H–40Ca
X 2Σ+
4,277
0,200 25
1H–58Ni
X 2Δ
7,700
0,147 56
1H–64Zn
X 2Σ+
6,679
0,159 49
1H–81Br
X 1Σ+
8,465
0,141 44
1H–115In
X 1Σ+
4,994
0,1838
1H–138Ba
X 2Σ+
3,3828
0,223 17
1H–174Yb
X 2Σ+
3,9930
0,2053
1H–205Tl
X 1Σ+
4,806
0,1870
Valeurs tirées de Huber, K. P. et G. Herzberg, Molecular Spectra and Molecular Structure IV. Constants of Diatomic Molecules, Van Nostrand Reinhold Co., New York, 1979.
Problèmes avec VR Molécules
-
Placez VR Molécules à la page 3â. Notez dans un tableau semblable à celui qui apparaît ci-dessous les valeurs de l'énergie pour les 6 premières valeurs non nulles du nombre quantique J
J
0
1
2
3
4
5
6
E (cm–1)
0
ΔE
–
Δ(ΔE)
–
L’énergie augmente-t-elle de manière proportionnelle aux valeurs de J ?
Allez plus loin dans le traitement des données et calculez les différences d’énergie entre les valeurs successives de J. Ces valeurs sont-elles proportionnelles aux valeurs de J ?
Finalement, calculez les deuxièmes différences, Δ(ΔE) = ΔE(J) – ΔE(J–1).
Que concluez-vous? Corrigé -
Placez VR Molécules à la page 2. En observant attentivement les mouvements des deux molécules, ou encore en utilisant la petite horloge en bas à droite de VR Molécules, essayez de chiffrer approximativement le rapport des vitesses de rotation de ces molécules, pour un même nombre quantique. Déterminez également le rapport des énergies des deux molécules.
Comment ces rapports se comparent-ils avec celui des masses réduites?
Corrigé -
Placez VR Molécules à la page 5, qui présente (en deux exemplaires) la molécule DCl, soit une molécule HCl où l'hydrogène a été remplacé par son isotope de masse 2, le deutérium. Celui-ci possède un neutron excédentaire, représenté par le point noir au centre de l'atome.
En faisant varier l'énergie de rotation et en activant si nécessaire la correction d'énergie appropriée, déterminez les valeurs des constantes D et B pour cette molécule. Corrigé -
Placez VR Molécules à la page 6, qui présente la molécule d'hydrogène. Activez la correction liée à la distorsion centrifuge et examinez comment varie l'énergie en fonction du nombre quantique J. Remarquez-vous quelque chose d'étrange?
Le phénomène en question provient des limites du modèle utilisé pour la simulation VR Molécules, qui inclut, si on l'active bien sûr, le terme de correction pour distorsion centrifuge décrit dans le module. Cependant, celui-ci n'est que le premier terme d'une série de corrections faisant intervenir les puissances de J (J+1).
Les deux premiers termes de cette série s'écrivent :ΔEcentrifuge (J) = – DJ 2 (J+1)2 + HJ 3 (J+1)3
Le terme contenant le facteur H, beaucoup plus petit que D, entraîne généralement une correction négligeable... sauf, visiblement, pour l'hydrogène. Cette molécule est celle qui possède le moment d'inertie le plus faible; elle présente donc les constantes de rotation les plus importantes. La prise en compte du terme cubique devient nécessaire, aux valeurs de J élevées, pour contrer la valeur excessive du terme quadratique.
À partir de ce que vous avez constaté en observant le comportement étrange du modèle, pouvez-vous estimer l'ordre de grandeur de la constante H pour la molécule d'hydrogène? Corrigé
Corrigés
-
Les raies rotationnelles correspondent aux transitions effectuées par la molécule entre ses niveaux de rotation. Il est donc nécessaire de calculer l’énergie de ces niveaux de rotation, F(J), puis de calculer les différences d'énergie entre ces niveaux pour obtenir les énergies des transitions. Les valeurs de F(J) sont reliées aux valeurs de la constante rotationnelle B et de la constante de distorsion centrifuge D de la molécule à travers la relation :
F(J) = BJ (J +1) – DJ 2 (J +1)
La valeur relative des deux constantes est indiquée, il suffit donc de calculer la valeur de la constante B. Cette constante rotationnelle est reliée au moment d’inertie de la molécule :
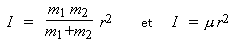
puisque μ est la masse réduite. En se rappelant que les masses des atomes de chlore et de fluor sont respectivement de 35,5 et de 19 g/mole, calculons la valeur de I dans le système SI :
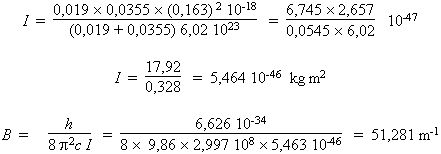
B = 0,513 cm–1
On peut dès maintenant établir l'énergie de chacun des niveaux J; en remplaçant B et D par leur valeurs, on obtient :
J
F(J)
Énergie (cm–1)
0
0
0
1
2 B – 4 D
1,026 – 3,5 × 10–6 = 1,026
2
6 B – 36D
3,078 – 3,157 10–5 = 3,078
3
12 B – 144 D
6,156 – 1,26 × 10–4 = 6,156
4
20 B – 400 D
10,26 – 3,51 × 10–4 = 10,26
Ces calculs montrent que la correction pour la distorsion centrifuge est ici négligeable. Les transitions rotationnelles doivent obéir à la règle de sélection, ΔJ = ±1. En absorption, on aura donc comme transition les quatre transitions suivantes (ΔJ = +1) :
J + 1 ← J
Énergie (cm–1)
1 ← 0
1,026 – 0 = 1,026
2 ← 1
3,078 – 1,026 = 2,053
3 ← 2
6,156 – 3,078 = 3,078
4 ← 3
10,26 – 6,156 = 4,10
-
- Dans un spectre de rotation, la
séparation observée entre deux raies
consécutives est égale à deux
fois la constante de rotation :
2B = 41,9 cm–1.
Cette constante est elle-même liée au
moment d’inertie de la molécule. Dans le
système d'unités SI, on obtient :
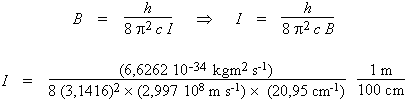
I = 1,336 × 10–47 kg · m2
- Le moment d’inertie est relié à
la distance internucléaire à travers la
relation I = μr2
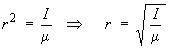
μ est la masse réduite du rotateur :
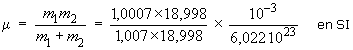
μ = 1,587 10–27 kg
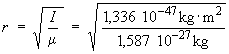
⇒ r = 0,917 10–10 m = 91,7 pm
- Le moment cinétique, P, peut
s'écrire : P = Iωoù
ω est la vitesse angulaire du rotateur.
On peut donc écrire :
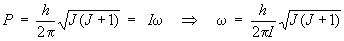
Donc :
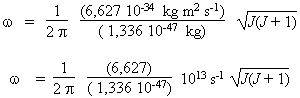
On peut maintenant compléter le tableau de résultats qui suit :
J
[ J(J+1) ]1/2
ω ( s–1)
0
0
0
1
21/2
1,116 × 1013
2
61/2
1,934 × 1013
3
121/2
2,735 × 1013
- Dans un spectre de rotation, la
séparation observée entre deux raies
consécutives est égale à deux
fois la constante de rotation :
2B = 41,9 cm–1.
Cette constante est elle-même liée au
moment d’inertie de la molécule. Dans le
système d'unités SI, on obtient :
-
On a vu que les raies d'absorption qui correspondent aux transitions rotationnelles sont espacées d'une distance (énergie exprimée en cm–1) égale à 2 fois la valeur de la constante rotationnelle B (en ignorant l'effet de la distorsion centrifuge). En se rappelant les formules reliant cette constante B, le moment d'inertie I et la longueur de la liaison r, on trouve :
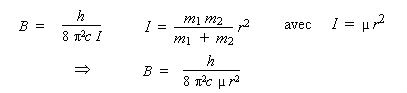
Si la valeur de r est multipliée par un facteur 10, la valeur de B est divisée par un facteur 100. L'espace, l'énergie entre deux raies, est donc divisé par le même facteur 100. Le spectre de rotation serait donc fortement affecté. Tout se passerait comme si ce spectre était compressé d'un facteur 100.
-
- Le problème revient à
employer les formules utilisées
précédemment :
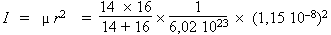
I = 1,64 10 –39 g · cm2
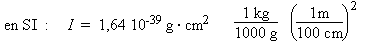
I = 1,64 × 10–46 kg · m2
- Le moment d'inertie venant d'être
calculé, on peut calculer la valeur de la
constante rotationnelle :
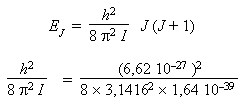
E = 3,38 × 10–16 ergs
E = 3,38 × 10–23 joules
On peut maintenant, en répétant les calculs pour différentes valeur de J, compléter le tableau suivant :
J
J (J + 1)
EJ
(ergs/molécule)EJ
(ergs/mole)EJ
(J/mol)1
2
6,76 × 10–16
40,8 × 107
40,8
2
6
20,34 × 10–16
122,4 × 107
122,4
3
12
40,68 × 10–16
244,8 × 107
244,8
4
20
67,78 × 10–16
408 × 107
408
- L'énergie de la transition entre deux
niveaux est évidemment égale à la
différence d'énergie entre ces niveaux.
Par exemple :
E2 – E1 = 122,4 – 40,8 = 81,6 J/mol.
Pour exprimer cette énergie en nombre d'ondes, il faut se rappeler que
 = E/hc,
où E est l'énergie d'un photon,
donc l'énergie perdue par une seule
molécule. On obtient ainsi :
= E/hc,
où E est l'énergie d'un photon,
donc l'énergie perdue par une seule
molécule. On obtient ainsi :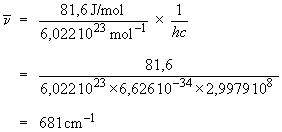
- Le problème revient à
employer les formules utilisées
précédemment :
-
On peut raisonnablement penser que la longueur de la liaison r (H–37Cl) est identique à r (H–35Cl).
Le moment d'inertie est I = μr2. Par ailleurs, la constante de rotation B est telle que :
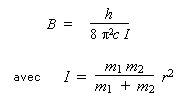
La solution du problème peut être obtenue en calculant pour chacune des deux molécules isotopiques sa valeur de B. Comme la longueur de la liaison n'est pas indiquée, on obtiendra les valeurs de B35 et de B37 avec un paramètre r. En faisant le rapport des deux valeurs de B ainsi obtenues, le paramètre r disparaîtra, et de la valeur de la constante B35, on obtiendra la valeur de la constante B37. Cette méthode exige de faire deux fois le même calcul. Cela n'est pas nécessaire et peut donc être évité en réécrivant la formule précédente. En posant m1 la masse de l'atome d'hydrogène et m2 la masse de l'atome de chlore, on peut en effet écrire :
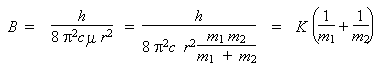
K est une constante de proportionnalité. Donc,

D'où
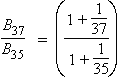
ou encore, en utilisant la loi des proportions :
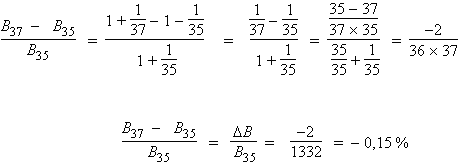
B37 – B35 = ΔB = 10,34 × 0,15 % = 0,0155 cm–1
et B37 = 10,34 – 0,0155 = 10,325 cm–1
-
L'énergie d'un niveau quelconque d'un rotateur rigide (pas de distorsion centrifuge, ou encore D = 0) est donnée par la relation :
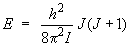
Le niveau J = 8 a donc une énergie telle que :
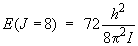
et l'énergie du niveau J = 9 est telle que :
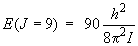
La différence d'énergie entre les deux niveaux est donc égale à :
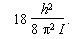
L'énergie de la transition est donc :
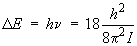
D'où :
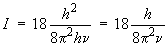
De cette relation, connaissant la fréquence de la transition et la constante de Planck, on obtient la valeur de I dans chacun des cas. Le calcul est exprimé avec les unités SI.
- 85Rb79Br
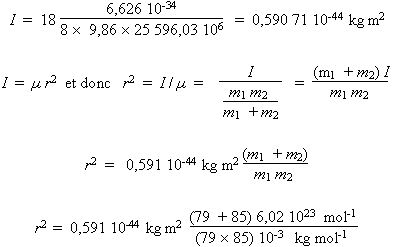
r2 = 0,868 50 × 10–19 m 2
r = 247 pm
- 87Rb79Br
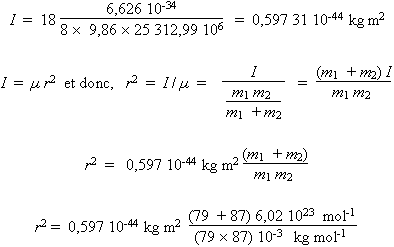
r2 = 0,868 47 × 10–19 m2
r = 247 pm
- 85Rb81Br
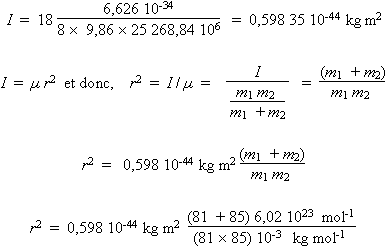
r2 = 0,858 72 × 10–19 m2
r = 293 pm
- 85Rb79Br
-
On sait que la constante rotationnelle est telle que
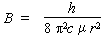
B est donc bien une fonction de 1 /μr2 où μ, la masse réduite, est telle que :
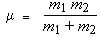
On constate que la valeur de la masse réduite est presque constante, variant entre 0,93 et 0,995 pour l'ensemble des molécules du tableau; on peut donc considérer que B est une fonction de 1 / r2 seulement.
La solution du problème est relativement simple. En utilisant un chiffrier comme Excel on obtient le tableau de valeurs et le graphe qui suivent montrant la variation de B en fonction de 1 / r2.
Molécule
B (cm–1)
re (nm)
1 / r2
1H–14N
16,699
0,103 62
93,13
1H–16O
18,911
0,096 97
106,3
1H–19F
20,956
0,091 68
118,9
1H–24Mg
5,8257
0,172 97
033,4
1H–32S
9,46
0,1341
55,6
1H–35Cl
10,59
0,1274
61,6
1H–40Ca
4,277
0,200 25
25,0
1H–58Ni
7,700
0,147 56
45,9
1H–64Zn
6,679
0,159 49
39,3
1H–81Br
8,465
0,141 44
50,0
1H–115In
4,994
0,1838
29,6
1H–138Ba
3,3828
0,223 17
20,1
1H–174Yb
3,9930
0,2053
23,7
1H–205Tl
4,806
0,1870
28,6
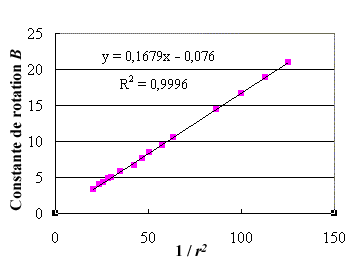
L'équation de la droite B = f (1/r2) est :
y = –0,0761 + 0,16788 x avec R 2 = 9,9996
où y est exprimé en cm–1 et x en nm–2.
La pente de cette droite, notée b, qui a pour unités des cm–1 nm2, est reliée au rapport h/c :
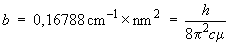
On peut donc calculer (c'est-à-dire obtenir expérimentalement) le rapport h/c.
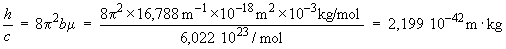
ce qui est très proche de la valeur directement calculée à partir des valeurs admises des constantes h et c, soit 2,210 921 10–42 m · kg.
Corrigés des problèmes avec VR Molécules
J
0123456E(cm–1)
0
20,88
62,64
125,3
208,8
313,2
438,5
ΔE
–
20,88
41,76
62,9
83,5
104,4
125,3
Δ(ΔE)
–
20,88
20,88
21,1
20,6
20,9
21,1
On remarque que les valeurs de l'énergie (première ligne de données du tableau) n'augmentent pas proportionnellement au nombre J; c'est le cas cependant pour les différences ΔE. Finalement, on constate que les deuxièmes différences, Δ(ΔE), sont constantes (dans la mesure permise par le nombre de chiffres significatifs). Comme ΔE représente la fréquence de la transition entre deux niveaux de rotation voisins, on en conclut que les fréquences de transition successives du spectre de rotation seront également espacées.
-
On peut mesurer les valeurs suivantes pour J = 25 :
HCl : 10 tours en 0,44 ps environ, soit 23 tours/ps, ou 2,3 × 1013 tours/seconde;
O2: 1 tour en 0,33 ps environ, soit 3,0 tours/ps, ou 3,0 × 1013 tours/seconde.
Le rapport entre les vitesses de rotation de HCl et de O2 est donc d'environ 7,7.
Par ailleurs, le rapport des énergies, soit E(HCl) / E(O2), est égal à 6786 / 929,5 = 7,3.
Ces deux rapports sont proches de l'inverse du rapport des masses réduites des molécules, soit μ(O2) / μ(HCl) = 8 / 1,03 = 7,8. Ces résultats s'expliquent par le fait que la distance entre les atomes est sensiblement la même dans les deux molécules. -
En l'absence de distorsion centrifuge, l'énergie du niveau J est donnée en unités de nombre d'ondes par :
F(J) = BJ (J+1)La valeur de B peut donc être déterminée à partir de celle de l'énergie pour un niveau J quelconque. Pour un maximum de précision, prenons le niveau J = 30; on trouve alors :
B = F(30) / (30×31) = 5015 / 930 = 5,39 cm–1
Pour déterminer la valeur de la constante D, il faut activer la correction de distorsion centrifuge pour la molécule de gauche. Si la valeur de la constante B est connue, une seule valeur d'énergie est alors requise pour déterminer la valeur de D.
D'après l'équation 1.11, on a en effet :DJ 2 (J+1)2 = BJ (J+1) – F(J)
où F(J) est la valeur incluant la correction et BJ (J+1) la valeur sans correction. On obtient, toujours en considérant J = 30 :
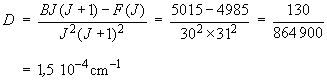
-
L'énergie de rotation, au lieu d'augmenter constamment avec le nombre J, atteint une valeur maximum d'environ 19 000 cm–1 à J = 25, pour diminuer par la suite. La correction pour distorsion centrifuge, qui inclut uniquement le premier terme, est donc trop grande; à J = 30, elle réduit l'énergie de 55 000 à 15 000 cm–1.
On peut estimer l'ordre de grandeur de la constante H si l'on fait l'hypothèse que le terme qui lui est associé devrait ramener la valeur de l'énergie à une valeur beaucoup plus proche de la valeur non corrigée. On supposera qu'à J = 30 cette valeur serait de l'ordre de 50 000 cm–1. On pourrait supposer une valeur différente, par exemple 40 000 cm–1, mais comme on cherche un ordre de grandeur, cela ne changerait pas vraiment le résultat.
Le second terme de correction devrait donc ajouter à la valeur corrigée au premier ordre environ 35 000 cm–1, ce qui permet d'écrire :
H ≈ 35 000 / J 3 (J+1)3 = 35 000 / (8 × 108) ≈ 4 × 10–5 cm–1
Notons que la valeur réelle de cette constante est 4,7 × 10–5 cm–1.